cjc0117
- 91
- 1
I tried posting this question in this forum a couple of weeks ago, but didn't get an answer to my question. I'm going to try posting it again using the formatting template so that it is hopefully clearer. I am also not sure if this is the right forum to be posting this in. It is a problem I ran into for one of my projects at work, rather than a homework question, and I am an engineer, not a physicist. Nevertheless, I thought this had more of a "homework feel" to it, and I noticed that most error propagation threads seem to be in the Physics homework forum. I don't think the problem requires any depth of engineering knowledge. I'm just trying to figure out why my two approaches to calculating a value from measured quantities do not result in the same value for propagated error.
1. Homework Statement
I am trying to find the error propagated by calculating the sum of a set of mass flow rates collected over the same length of time. The sum of mass flow rates can be calculated with two approaches, since the collection time is the same for all of them. Approach (1) is adding up all of the individual mass flow rates, and Approach (2) is adding up all of the masses and then dividing by the collection time. However, when I use standard error propagation formulas (http://lectureonline.cl.msu.edu/~mmp/labs/error/e2.htm) to derive an expression for the error in the sum of mass flow rates, I get two different answers depending on which of the two above approaches I use.
I have calculated the mass, m_{i}, of liquid exiting the outlet of stream i for n number of streams over a measured time period of t, by measuring the mass of liquid + container, M_{1,i}, and subtracting from that the measurement for the mass of the container, M_{2,i}. The masses M_{1,i} and M_{2,i} both have the same measurement error (the error of the scale), which is the same for all n streams. Thus, the error in m_{i} is the same for all streams. The liquid from each stream was collected simultaneously in separate containers (i.e., there are n containers for n streams), therefore, there is only one t measurement for all of them. The mass flow rate, \dot{m}_{i}, is calculated for each stream i by dividing the mass of the stream, m_{i}, by the collection time, t.
The above explanation can be summarized as follows:
Objective: Show that if \sum^n_{i=1}\dot{m}_i=\frac{\sum^n_{i=1}m_{i}}{t} then \delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\delta{\left(\frac{\sum^n_{i=1}m_{i}}{t}\right)}
Define: M_{1,i}\ \mbox{and}\ M_{2,i}\ \mbox{are measured masses}\\\ \\m_{i}=M_{1,i}-M_{2,i}\ \mbox{for all}\ i\\\ \\\dot{m_{i}}=\frac{m_{i}}{t}\ \mbox{for all}\ i
Given: t=const.\ \mbox{(i.e., all masses were collected over the same time period)}\\\delta{M_{1,i}}=\delta{M_{2,i}}=\delta{M}=const.\ \mbox{for all}\ i
[/B]
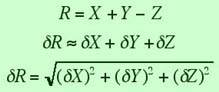
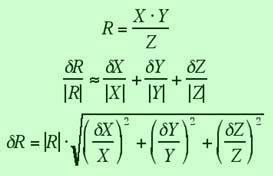
From http://lectureonline.cl.msu.edu/~mmp/labs/error/e2.htm
First, I show that \sum^n_{i=1}\dot{m}_i=\frac{\sum^n_{i=1}m_{i}}{t}:
\sum^n_{i=1}\dot{m}_i\stackrel{?}{=}\frac{\sum^n_{i=1}m_{i}}{t}\\\ \\\dot{m}_{1}+\dot{m}_{2}+...+\dot{m}_{n}\stackrel{?}{=}\frac{\sum^n_{i=1}m_{i}}{t}\\\ \\\frac{m_{1}}{t}+\frac{m_{2}}{t}+...+\frac{m_{n}}{t}\stackrel{?}{=}\frac{\sum^n_{i=1}m_{i}}{t}\\\ \\\frac{1}{t}\left(m_{1}+m_{2}+...+m_{n}\right)\stackrel{?}{=}\frac{\sum^n_{i=1}m_{i}}{t}\\\ \\\frac{\sum^n_{i=1}m_{i}}{t}=\frac{\sum^n_{i=1}m_{i}}{t}
Next, I calculate \delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)} and \delta{\left(\frac{\sum^n_{i=1}m_{i}}{t}\right)} in an attempt to show that they are equal:
\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\sqrt{\sum^n_{i=1}\left(\delta{\dot{m}_{i}}\right)^2}\\\ \\\ \ \ \ \ \ \ \ \ \ \delta{\dot{m}_{i}}=\dot{m}_{i}\sqrt{\left(\frac{\delta{m_{i}}}{m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2}\\\ \\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \delta{m_{i}}=\sqrt{\left(\delta{M_{1,i}}\right)^2+\left(\delta{M_{2,i}}\right)^2}=\sqrt{2\left(\delta{M}\right)^2}=\sqrt{2}\delta{M}=\delta{m}=const.\ \mbox{for all}\ i\\\ \\\ \ \ \ \ \ \ \ \ \ \delta{\dot{m}_{i}}=\dot{m}_{i}\sqrt{\left(\frac{\delta{m_{i}}}{m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2}=\dot{m}_{i}\sqrt{\left(\frac{\delta{m}}{m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2}=\dot{m}_{i}\sqrt{2\left(\frac{\delta{M}}{m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2}\\\ \\\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\sqrt{\sum^n_{i=1}\dot{m}_{i}^2\left[2\left(\frac{\delta{M}}{m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2\right]}\\\ \\\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\sqrt{\sum^n_{i=1}\left(\frac{m_{i}}{t}\right)^2\left[2\left(\frac{\delta{M}}{m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2\right]}\\\ \\\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\sqrt{\frac{1}{t^2}\sum^n_{i=1}m_{i}^2\left[2\left(\frac{\delta{M}}{m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2\right]}\\\ \\\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\frac{1}{t}\sqrt{\sum^n_{i=1}\left[2\left(\delta{M}\right)^2+m_{i}^2\left(\frac{\delta{t}}{t}\right)^2\right]}\\\ \\\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\frac{1}{t}\sqrt{\sum^n_{i=1}2\left(\delta{M}\right)^2+\sum^n_{i=1}m_{i}^2\left(\frac{\delta{t}}{t}\right)^2}\\\ \\\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\frac{1}{t}\sqrt{2n\left(\delta{M}\right)^2+\sum^n_{i=1}m_{i}^2\left(\frac{\delta{t}}{t}\right)^2}\\\ \\\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\frac{\sum^n_{i=1}m_{i}}{t}\sqrt{2n\left(\frac{\delta{M}}{\sum^n_{i=1}m_{i}}\right)^2+\frac{\sum^n_{i=1}m_{i}^2}{\left(\sum^n_{i=1}m_{i}\right)^2}\left(\frac{\delta{t}}{t}\right)^2}\ \ \ \ \ \ \ \ \ \ \mbox{*(EQN. 1)*}\\\ \\\ \\\delta{\left(\frac{\sum^n_{i=1}m_{i}}{t}\right)}=\frac{\sum^n_{i=1}m_{i}}{t}\sqrt{\left(\frac{\delta{\left(\sum^n_{i=1}m_{i}\right)}}{\sum^n_{i=1}m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2}\\\ \\\ \ \ \ \ \ \ \ \ \ \delta{\left(\sum^n_{i=1}m_{i}\right)}=\sqrt{\sum^n_{i=1}\left(\delta{m_{i}}\right)^2}\\\ \\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \delta{m_{i}}=\sqrt{\left(\delta{M_{1,i}}\right)^2+\left(\delta{M_{2,i}}\right)^2}=\sqrt{2\left(\delta{M}\right)^2}=\sqrt{2}\delta{M}=\delta{m}=const.\ \mbox{for all}\ i\\\ \\\ \ \ \ \ \ \ \ \ \ \delta{\left(\sum^n_{i=1}m_{i}\right)}=\sqrt{\sum^n_{i=1}\left(\delta{m_{i}}\right)^2}=\sqrt{\sum^n_{i=1}\left(\delta{m}\right)^2}=\sqrt{n\left(\delta{m}\right)^2}=\sqrt{2n}\delta{M}\\\ \\\delta{\left(\frac{\sum^n_{i=1}m_{i}}{t}\right)}=\frac{\sum^n_{i=1}m_{i}}{t}\sqrt{\left(\frac{\sqrt{2n}\delta{M}}{\sum^n_{i=1}m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2}\\\ \\\delta{\left(\frac{\sum^n_{i=1}m_{i}}{t}\right)}=\frac{\sum^n_{i=1}m_{i}}{t}\sqrt{2n\left(\frac{\delta{M}}{\sum^n_{i=1}m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2}\ \ \ \ \ \ \ \ \ \ \mbox{*(EQN. 2)*}
(EQN. 1) is not equivalent to (EQN. 2), because the second term in the radical is multiplied by the extra \frac{\sum^n_{i=1}m_{i}^2}{\left(\sum^n_{i=1}m_{i}\right)^2} term. This would suggest that \delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}\neq\delta{\left(\frac{\sum^n_{i=1}m_{i}}{t}\right)}. However, if \sum^n_{i=1}\dot{m}_i=\frac{\sum^n_{i=1}m_{i}}{t} then why shouldn't \delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\delta{\left(\frac{\sum^n_{i=1}m_{i}}{t}\right)}? Where have I gone wrong?
1. Homework Statement
I am trying to find the error propagated by calculating the sum of a set of mass flow rates collected over the same length of time. The sum of mass flow rates can be calculated with two approaches, since the collection time is the same for all of them. Approach (1) is adding up all of the individual mass flow rates, and Approach (2) is adding up all of the masses and then dividing by the collection time. However, when I use standard error propagation formulas (http://lectureonline.cl.msu.edu/~mmp/labs/error/e2.htm) to derive an expression for the error in the sum of mass flow rates, I get two different answers depending on which of the two above approaches I use.
I have calculated the mass, m_{i}, of liquid exiting the outlet of stream i for n number of streams over a measured time period of t, by measuring the mass of liquid + container, M_{1,i}, and subtracting from that the measurement for the mass of the container, M_{2,i}. The masses M_{1,i} and M_{2,i} both have the same measurement error (the error of the scale), which is the same for all n streams. Thus, the error in m_{i} is the same for all streams. The liquid from each stream was collected simultaneously in separate containers (i.e., there are n containers for n streams), therefore, there is only one t measurement for all of them. The mass flow rate, \dot{m}_{i}, is calculated for each stream i by dividing the mass of the stream, m_{i}, by the collection time, t.
The above explanation can be summarized as follows:
Objective: Show that if \sum^n_{i=1}\dot{m}_i=\frac{\sum^n_{i=1}m_{i}}{t} then \delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\delta{\left(\frac{\sum^n_{i=1}m_{i}}{t}\right)}
Define: M_{1,i}\ \mbox{and}\ M_{2,i}\ \mbox{are measured masses}\\\ \\m_{i}=M_{1,i}-M_{2,i}\ \mbox{for all}\ i\\\ \\\dot{m_{i}}=\frac{m_{i}}{t}\ \mbox{for all}\ i
Given: t=const.\ \mbox{(i.e., all masses were collected over the same time period)}\\\delta{M_{1,i}}=\delta{M_{2,i}}=\delta{M}=const.\ \mbox{for all}\ i
Homework Equations
[/B]
From http://lectureonline.cl.msu.edu/~mmp/labs/error/e2.htm
The Attempt at a Solution
First, I show that \sum^n_{i=1}\dot{m}_i=\frac{\sum^n_{i=1}m_{i}}{t}:
\sum^n_{i=1}\dot{m}_i\stackrel{?}{=}\frac{\sum^n_{i=1}m_{i}}{t}\\\ \\\dot{m}_{1}+\dot{m}_{2}+...+\dot{m}_{n}\stackrel{?}{=}\frac{\sum^n_{i=1}m_{i}}{t}\\\ \\\frac{m_{1}}{t}+\frac{m_{2}}{t}+...+\frac{m_{n}}{t}\stackrel{?}{=}\frac{\sum^n_{i=1}m_{i}}{t}\\\ \\\frac{1}{t}\left(m_{1}+m_{2}+...+m_{n}\right)\stackrel{?}{=}\frac{\sum^n_{i=1}m_{i}}{t}\\\ \\\frac{\sum^n_{i=1}m_{i}}{t}=\frac{\sum^n_{i=1}m_{i}}{t}
Next, I calculate \delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)} and \delta{\left(\frac{\sum^n_{i=1}m_{i}}{t}\right)} in an attempt to show that they are equal:
\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\sqrt{\sum^n_{i=1}\left(\delta{\dot{m}_{i}}\right)^2}\\\ \\\ \ \ \ \ \ \ \ \ \ \delta{\dot{m}_{i}}=\dot{m}_{i}\sqrt{\left(\frac{\delta{m_{i}}}{m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2}\\\ \\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \delta{m_{i}}=\sqrt{\left(\delta{M_{1,i}}\right)^2+\left(\delta{M_{2,i}}\right)^2}=\sqrt{2\left(\delta{M}\right)^2}=\sqrt{2}\delta{M}=\delta{m}=const.\ \mbox{for all}\ i\\\ \\\ \ \ \ \ \ \ \ \ \ \delta{\dot{m}_{i}}=\dot{m}_{i}\sqrt{\left(\frac{\delta{m_{i}}}{m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2}=\dot{m}_{i}\sqrt{\left(\frac{\delta{m}}{m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2}=\dot{m}_{i}\sqrt{2\left(\frac{\delta{M}}{m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2}\\\ \\\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\sqrt{\sum^n_{i=1}\dot{m}_{i}^2\left[2\left(\frac{\delta{M}}{m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2\right]}\\\ \\\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\sqrt{\sum^n_{i=1}\left(\frac{m_{i}}{t}\right)^2\left[2\left(\frac{\delta{M}}{m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2\right]}\\\ \\\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\sqrt{\frac{1}{t^2}\sum^n_{i=1}m_{i}^2\left[2\left(\frac{\delta{M}}{m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2\right]}\\\ \\\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\frac{1}{t}\sqrt{\sum^n_{i=1}\left[2\left(\delta{M}\right)^2+m_{i}^2\left(\frac{\delta{t}}{t}\right)^2\right]}\\\ \\\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\frac{1}{t}\sqrt{\sum^n_{i=1}2\left(\delta{M}\right)^2+\sum^n_{i=1}m_{i}^2\left(\frac{\delta{t}}{t}\right)^2}\\\ \\\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\frac{1}{t}\sqrt{2n\left(\delta{M}\right)^2+\sum^n_{i=1}m_{i}^2\left(\frac{\delta{t}}{t}\right)^2}\\\ \\\delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\frac{\sum^n_{i=1}m_{i}}{t}\sqrt{2n\left(\frac{\delta{M}}{\sum^n_{i=1}m_{i}}\right)^2+\frac{\sum^n_{i=1}m_{i}^2}{\left(\sum^n_{i=1}m_{i}\right)^2}\left(\frac{\delta{t}}{t}\right)^2}\ \ \ \ \ \ \ \ \ \ \mbox{*(EQN. 1)*}\\\ \\\ \\\delta{\left(\frac{\sum^n_{i=1}m_{i}}{t}\right)}=\frac{\sum^n_{i=1}m_{i}}{t}\sqrt{\left(\frac{\delta{\left(\sum^n_{i=1}m_{i}\right)}}{\sum^n_{i=1}m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2}\\\ \\\ \ \ \ \ \ \ \ \ \ \delta{\left(\sum^n_{i=1}m_{i}\right)}=\sqrt{\sum^n_{i=1}\left(\delta{m_{i}}\right)^2}\\\ \\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \delta{m_{i}}=\sqrt{\left(\delta{M_{1,i}}\right)^2+\left(\delta{M_{2,i}}\right)^2}=\sqrt{2\left(\delta{M}\right)^2}=\sqrt{2}\delta{M}=\delta{m}=const.\ \mbox{for all}\ i\\\ \\\ \ \ \ \ \ \ \ \ \ \delta{\left(\sum^n_{i=1}m_{i}\right)}=\sqrt{\sum^n_{i=1}\left(\delta{m_{i}}\right)^2}=\sqrt{\sum^n_{i=1}\left(\delta{m}\right)^2}=\sqrt{n\left(\delta{m}\right)^2}=\sqrt{2n}\delta{M}\\\ \\\delta{\left(\frac{\sum^n_{i=1}m_{i}}{t}\right)}=\frac{\sum^n_{i=1}m_{i}}{t}\sqrt{\left(\frac{\sqrt{2n}\delta{M}}{\sum^n_{i=1}m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2}\\\ \\\delta{\left(\frac{\sum^n_{i=1}m_{i}}{t}\right)}=\frac{\sum^n_{i=1}m_{i}}{t}\sqrt{2n\left(\frac{\delta{M}}{\sum^n_{i=1}m_{i}}\right)^2+\left(\frac{\delta{t}}{t}\right)^2}\ \ \ \ \ \ \ \ \ \ \mbox{*(EQN. 2)*}
(EQN. 1) is not equivalent to (EQN. 2), because the second term in the radical is multiplied by the extra \frac{\sum^n_{i=1}m_{i}^2}{\left(\sum^n_{i=1}m_{i}\right)^2} term. This would suggest that \delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}\neq\delta{\left(\frac{\sum^n_{i=1}m_{i}}{t}\right)}. However, if \sum^n_{i=1}\dot{m}_i=\frac{\sum^n_{i=1}m_{i}}{t} then why shouldn't \delta{\left(\sum^n_{i=1}\dot{m}_{i}\right)}=\delta{\left(\frac{\sum^n_{i=1}m_{i}}{t}\right)}? Where have I gone wrong?