Euler beam dynamic equation under point load

[Aladdin123]

Hi
So the problem I have is I want to get the equation of motion of a vibrating beam under a nonlinear "Point" force.
The equation would be like this for a distributed load (Which is not the case)

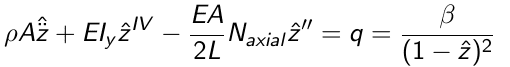
But I want the load to be at a point at x=L
So I have to options. Add an impulse dirac function multiplied by the beta (Causes numerical errors for my solver), or define the force as follows:

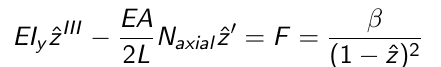
Thus

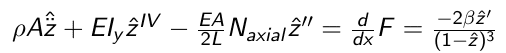
Which one is correct or if both wrong what do I do.
Also even if one of them is correct, any better options? (The above cases messes up my numerical solver)

Note: Obviously, z is a function of (x,t) and also beta is a function of (t)

 

[Nidum]

How is the beam supported ?

What do you mean by non linear point load ? Has it got any physical interpretation or any defining equation ?

Are you looking for a small deflection or large deflection solution ?