I Evaluating Scattering Integral

[Waxterzz]

Hi,

I really don't have a clue to solve this.

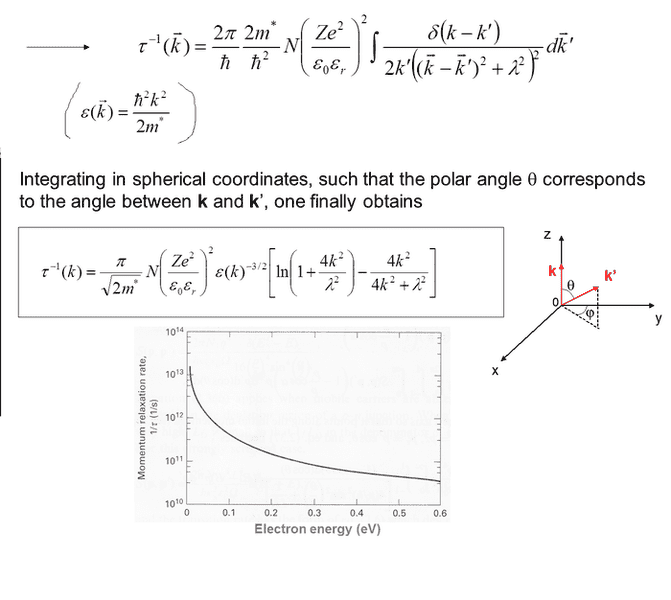I tried something like the dirac function identity:

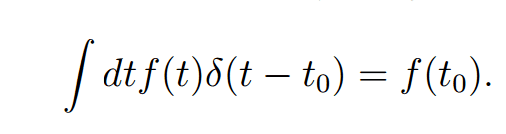
But then I saw it's dk' not dk' and couldn't got it straight.

Can someone help me with this?

 

[DrClaude]

As it is said, you have to change to spherical coordinates. The Dirac delta will then only affect the integral over r.

 

[Waxterzz]

As it is said, you have to change to spherical coordinates. The Dirac delta will then only affect the integral over r.

I don't see it. dk' is not a volume element?

 

[Waxterzz]

dk' is a vector. Then I have an integral comprising of 3 terms each involving unit vectors.

I really don't have a clue.

 

[Waxterzz]

Wait wait, I am extremely confused.

I just have to integrate over the k' first?

 

[Waxterzz]

Mr

As it is said, you have to change to spherical coordinates. The Dirac delta will then only affect the integral over r.

6 hours and I still have no clue, can you please hold my hand and solve it with me. I mean, just say what I have to do, I will solve it, but give me instructions.

I mean what's the deal with the dirac function and the dk', it's supposed to be a volume element and the dirac term, why isn't it delta(k-k')

 

[blue_leaf77]

$d\vec{k}$ is a volume element. Write it as a volume element in spherical coordinate. To make the integrand even more transparent, use the cosine law to express $|\vec{k}-\vec{k'}|^2$ in terms of $k$, $k'$, and $\theta$.

 

[Waxterzz]

$d\vec{k}$ is a volume element. Write it as a volume element in spherical coordinate. To make the integrand even more transparent, use the cosine law to express $|\vec{k}-\vec{k'}|^2$ in terms of $k$, $k'$, and $\theta$.

How come dk' is a volume element, it's the derivative of a vector. Most textbooks, the volume element is called a d tau or a dV

My head is a mess. It's like I completely forgot how to calculus.

Good news: I know I'm wrong.

Really don't see it

 

[DrClaude]

What happened to the Dirac delta? You should do the integral over k' first.

 

[DrClaude]

How come dk' is a volume element, it's the derivative of a vector. Most textbooks, the volume element is called a d tau or a dV

It's not a derivative, it is an infinitesimal vector element.

 

[Waxterzz]

It's not a derivative, it is an infinitesimal vector element.

It's been this the whole time?, with r being k'

Ps: After this I'm going to finally learn LaTeX

 

[blue_leaf77]

Why did the Dirac delta disappear in the second equation from the last one?

 

[Waxterzz]

This is what I got uptil now, but I have to leave.

Thanks for help, give me feedback if you want to, and I will post update when I'm back, probably tomorrow. Thanks for the patience anyway!

 

[Waxterzz]

It's not a derivative, it is an infinitesimal vector element.

Why did the Dirac delta disappear in the second equation from the last one?

Hi,

Sorry for the late reply.

Hope this is somewhat more clear, because last post was a bit messy. Still haven't learned LaTex.

Is this valid?

I couldn't evaluatie the last integral, because of the square.

Do I need to use partial fractions?

Thanks

 

[Waxterzz]

Hi myself,

I found out I need to include something like 1- ( stuff going in the z direction after k scattering) / (stuff that would go in z direction if there was no scattering at all), so 1 - k' projected on z axis /k = 1 - (k cos theta) / k

Yes, I'm a noob.

So I'll start over. :')