ghost11
- 3
- 0
Hi guys
is the example true?
what will the clock 3 count when the light reach it
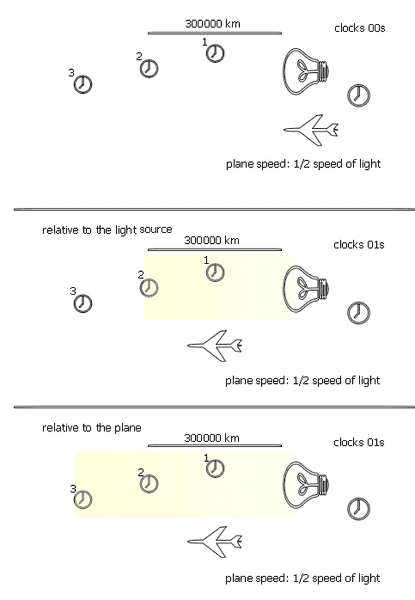
is the example true?
what will the clock 3 count when the light reach it
Last edited:
