DrMcDreamy
- 68
- 0
Homework Statement
This is a two part problem:
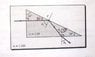
2) As shown in the figure, a light ray is incident normally on one face of a 26◦–64◦–90◦ block of dense flint glass (a prism) that immersed in water. Find the exit angle θ4 of the light ray (Assume the index of grass is 1.69, and that of water is 1.333.) Answer in units of ◦.
3) A substance is dissolved in the water to increase the index of refraction. At what value of n2 does total internal reflection cease at point P ?
Homework Equations
n1sin\theta1=n2sin\theta2
The Attempt at a Solution
My work:
I put in the answer to number 2 and it said its wrong. What I am doing wrong? Can you guys guide me through the problem? TIA!