Explanation of entropy only takes into account positions?

[dhruv8890]

Hi,

I've read several times an explanation of entropy that describes it something like "log of the number of states that are macroscopically indistinguishable". So the entropy of a system depends on the number of positions all the particles in the system can be in - right?

If a system is like this picture:

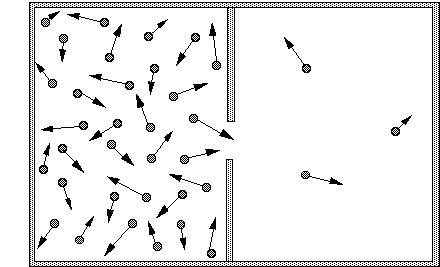
and the system goes to a state where there are equal number of particles, the entropy will have increased. If that's correct then the entropy of the system only takes into account the positions (or possible positions) of the particles involved. My question is - why doesn't entropy take into account momentum, temperature, energy etc. That information isn't available in "the number of macroscopically indistinguishable states".

If 2 pieces of the same material, at different temperatures is brought into contact, the system's entropy increases as the heat is transferred from one piece to the other. How did the number of macroscopically indistinguishable states increase? The energy of the one piece went down as the other's went up - does this affect entropy?

Thank you and I appreciate the help,
Dhruv

 

[Matterwave]

Momentum is indeed taken into account. The state that the particle may fill is in 6-dimensional phase space (3 for position, 3 for momentum).