gkirkland
- 11
- 0
Can someone please explain the below proof in more detail?

The part in particular which is confusing me is
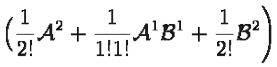
Thanks in advance!
The part in particular which is confusing me is
Thanks in advance!