shirel
- 38
- 0
Hi
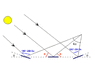
I've read about "light trails" in http://www.islandnet.com/~see/weather/elements/glitter.htm
but I didn't understand how they have calculated the 4a angle, and what really is the meaning of it.
I've read about "light trails" in http://www.islandnet.com/~see/weather/elements/glitter.htm
but I didn't understand how they have calculated the 4a angle, and what really is the meaning of it.