Exploring QFT: Is It Understandable?

[Tommy White]

TL;DR Summary

Or a "layperson's definition" of those quantities.

I understand that for the experts it (probably) involves a lot, for me complex, math.

But I wonder if there's a well .. simplified way to describe and understand this.

I'm not even sure whether it can be defined in QFT, but I got this from SE:

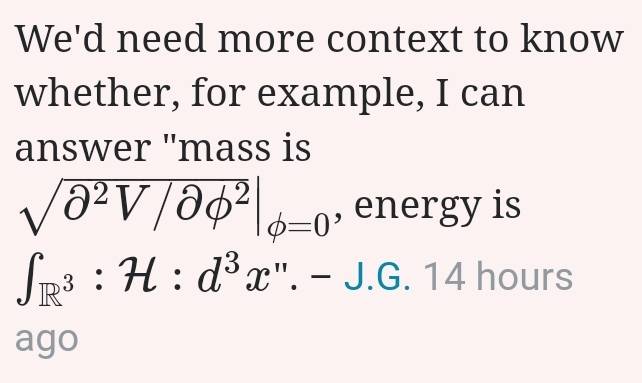
Which I don't understand. I'm not mathematically sophisticated enough for that.

 

[PeterDonis]

I got this from SE

Which is not a valid reference. You need to be looking at textbooks or peer-reviewed papers.

 

[PeterDonis]

I'm not even sure whether it can be defined in QFT

Do you understand how mass and energy are defined in classical physics?

 

[Tommy White]

Do you understand how mass and energy are defined in classical physics?

Yes, I understand that. As well as the mass-energy equivalence.

 

[PeterDonis]

Yes, I understand that. As well as the mass-energy equivalence.

So what do you understand "mass" and "energy" to mean in classical physics?

 

[Tommy White]

Which is not a valid reference. You need to be looking at textbooks or peer-reviewed papers.

Yes, that's true. I'll have to look it up later though. What about Wikipedia by the way?

 

[PeterDonis]

What about Wikipedia by the way?

Not a valid source for learning about this topic, or indeed about any scientific topic if you really want to understand the details. There are plenty of Wikipedia articles that do give reasonably accurate information about science topics, but the problem is that unless you are already knowledgeable about the topic you won't know which articles those are.

 

[Tommy White]

So what do you understand "mass" and "energy" to mean in classical physics?

Well I could write a lot about it. But I think understanding Einstein's paper "Does the inertia of a body depend on its energy content?" explains it quite well.

Which in a nutshell tells that the inertial mass of a body increases (or decreases) by the amount m=E/c^2 if its energy content increases (or decreases) by an amount E.

Though for photons/EM- radiation this does not apply (unless it's a photon gas).

 

[Tommy White]

Not a valid source for learning about this topic, or indeed about any scientific topic if you really want to understand the details. There are plenty of Wikipedia articles that do give reasonably accurate information about science topics, but the problem is that unless you are already knowledgeable about the topic you won't know which articles those are.

Ok, thank you.

 

[PeterDonis]

the inertial mass of a body increases (or decreases) by the amount m=E/c^2 if its energy content increases (or decreases) by an amount E.

Ok, so by "mass" you mean "inertial mass" and by "energy" you basically mean "energy content in the center of mass frame of the system", which is indeed basically the same as the inertial mass of the system.

Though for photons/EM- radiation this does not apply (unless it's a photon gas).

In the sense that the concept of "inertial mass" does not really apply to pure EM radiation, yes. (But, as you note, it does apply to radiation contained in a box made of matter.)

So, with that information, I can now try to clarify your question in this thread. Are you trying to understand how quantum physics deals with the concept of the inertial mass of a system?

 

[Tommy White]

Ok, so by "mass" you mean "inertial mass" and by "energy" you basically mean "energy content in the center of mass frame of the system", which is indeed basically the same as the inertial mass of the system.In the sense that the concept of "inertial mass" does not really apply to pure EM radiation, yes. (But, as you note, it does apply to radiation contained in a box made of matter.)

So, with that information, I can now try to clarify your question in this thread. Are you trying to understand how quantum physics deals with the concept of the inertial mass of a system?

Well, yes. But inertial mass, gravitational mass, rest mass, effective mass etc. is all the same: just mass, right? (And historically there was also transversal mass and longitudinal mass, electromagnetic mass, relativistic mass which is still used sometimes though. Those are things of the past so I'm not sure why I mention it). And in GR there Komar mass and ADM mass.

So all kinds of mass-terms or concepts of mass, which all have the same property that it has the resistance to a chance in velocity (though I'm not sure about the last two, but that's pherhaps for another question) .. but unlike energy.

And so I don't know if because E=mc^2, QM deals with the concept of energy the same as with (inertial) mass?

I'm a real layperson with QM and GR as well, though I understand that much better.

But anyway, yes if you'd like. All information would be welcome.

 

[PeterDonis]

inertial mass, gravitational mass, rest mass, effective mass etc. is all the same: just mass, right?

No.

According to GR, inertial mass and gravitational mass are the same, where here "gravitational mass" means what in more precise terminology would be called "passive" gravitational mass. Basically, this property determines how an object's trajectory in spacetime depends on its initial velocity and any forces it is subjected to. (Note that in GR gravity itself is not a force, and an object moving solely "due to gravity" is in free fall and feels no force, and has zero proper acceleration.)

Rest mass is the invariant length of an object's 4-momentum vector. It is conceptually distinct from inertial/gravitational mass, although in many scenarios they are numerically equivalent.

I'm not sure what you mean by "effective mass".

(And historically there was also transversal mass and longitudinal mass, electromagnetic mass, relativistic mass which is still used sometimes though. Those are things of the past so I'm not sure why I mention it).

Your hesitation is well founded. None of those concepts are useful in our best current models in physics.

And in GR there Komar mass and ADM mass.

Yes, which are both different from the above concepts, and different from each other. The most important difference between these concepts and the ones above is that Komar mass and ADM mass (and Bondi mass, which is different again) are global concepts, not local concepts, and are only valid in particular types of spacetimes.

all kinds of mass-terms or concepts of mass, which all have the same property that it has the resistance to a chance in velocity

No, they are not. See above.

unlike energy

I'm not sure why you say that, since previously you said the energy of a system was the same as its inertial mass.

I don't know if because E=mc^2

$E = mc^2$ is actually not a very useful equation. It can be viewed either as a simple tautology describing a conversion of units--i.e., a given quantity in energy units is the same as that quantity in mass units multiplied by the speed of light squared--or as a special case of the relativistic energy-momentum relation $E^2 - p^2 c^2 = m^2 c^4$, where $m$ is the rest mass (or invariant mass, which is a better term).

QM deals with the concept of energy the same as with (inertial) mass?

in QM in general, "energy" is an observable (mathematically it is described by an operator, the Hamiltonian). This observable would tell you the inertial properties of the system you are observing, so it could be taken as also telling you a system's inertial mass, but cases in QM in which that is relevant are rare.

In QFT, the term "mass" is usually used to describe an inherent property of particles (or more precisely quantum fields). In this usage it more or less corresponds with the classical concept of rest mass/invariant mass.

 

[Tommy White]

No.

According to GR, inertial mass and gravitational mass are the same, where here "gravitational mass" means what in more precise terminology would be called "passive" gravitational mass. Basically, this property determines how an object's trajectory in spacetime depends on its initial velocity and any forces it is subjected to. (Note that in GR gravity itself is not a force, and an object moving solely "due to gravity" is in free fall and feels no force, and has zero proper acceleration.)

Rest mass is the invariant length of an object's 4-momentum vector. It is conceptually distinct from inertial/gravitational mass, although in many scenarios they are numerically equivalent.

I'm not sure what you mean by "effective mass".Your hesitation is well founded. None of those concepts are useful in our best current models in physics.Yes, which are both different from the above concepts, and different from each other. The most important difference between these concepts and the ones above is that Komar mass and ADM mass (and Bondi mass, which is different again) are global concepts, not local concepts, and are only valid in particular types of spacetimes.No, they are not. See above.I'm not sure why you say that, since previously you said the energy of a system was the same as its inertial mass.$E = mc^2$ is actually not a very useful equation. It can be viewed either as a simple tautology describing a conversion of units--i.e., a given quantity in energy units is the same as that quantity in mass units multiplied by the speed of light squared--or as a special case of the relativistic energy-momentum relation $E^2 - p^2 c^2 = m^2 c^4$, where $m$ is the rest mass (or invariant mass, which is a better term).in QM in general, "energy" is an observable (mathematically it is described by an operator, the Hamiltonian). This observable would tell you the inertial properties of the system you are observing, so it could be taken as also telling you a system's inertial mass, but cases in QM in which that is relevant are rare.

In QFT, the term "mass" is usually used to describe an inherent property of particles (or more precisely quantum fields). In this usage it more or less corresponds with the classical concept of rest mass/invariant mass.

Ok, thanks very much!
Got to take it all in slowly though.

I thought inertial mass and gravitational mass were the same, because although inertial mass, passive gravitational mass and active gravitational mass are conceptually distinct, no experiment has ever unambiguously demonstrated any difference between them. .. But I guess the deeper meaning is different.

I mentioned "effective mass" because of my very limited understanding about it .. uhm according to QFT most elementary particles get there mass from the Higgs-field, slowing them down. Light is slowed down in a medium (glass) by giving photons a mass-term. And they become polaritons, but the principle is the same (as I'm told), that whether something interacts with the vacuum or with a medium slowing it down, it gets massive.

But I feel like mixing a lot of things up.

I wanted to send you a message, but .. I'm too tired now. Been up all night, so I feel like I am becoming incoherent.

Oh yes, I wanted to say that I had multiple questions this week. But they are all just solved and this a bit vague one was left. Which is a shame because I have a good feeling about this forum.

I have hundreds of questions, but don't want to be spoon fedded of course.

Sorry this is becoming a bit chat-like. But thanks again! (Really feels like a good forum.)

 

[vanhees71]

To really understand these very fundamental (an by no means trivial) questions, as far as they are known today, you need to understand the theory of (unitary ray) representations of the Poincare group. An excellent textbook about this is

R. U. Sexl and H. K. Urbantke, Relativity, Groups, Particles, Springer, Wien (2001).

 

[PeterDonis]

I thought inertial mass and gravitational mass were the same, because although inertial mass, passive gravitational mass and active gravitational mass are conceptually distinct, no experiment has ever unambiguously demonstrated any difference between them.

In GR, inertial mass and passive gravitational mass are not even conceptually distinct. Active gravitational mass is, and moreover, in GR it is not the same as inertial mass/passive gravitational mass. The GR counterpart of active gravitational mass, how an object behaves as a source of gravity, is the stress-energy tensor, which is not even a number, it's a tensor.

I mentioned "effective mass" because of my very limited understanding about it .. uhm according to QFT most elementary particles get there mass from the Higgs-field, slowing them down. Light is slowed down in a medium (glass) by giving photons a mass-term. And they become polaritons, but the principle is the same (as I'm told), that whether something interacts with the vacuum or with a medium slowing it down, it gets massive.

I've never seen "effective mass" used as a term to describe either of these things. Also, you're mixing up different things: the Higgs mechanism, which gives nonzero invariant mass to Standard Model particles, is not the same as the mechanism of how light behaves in a material medium.

 

[Tommy White]

To really understand these very fundamental (an by no means trivial) questions, as far as they are known today, you need to understand the theory of (unitary ray) representations of the Poincare group. An excellent textbook about this is

R. U. Sexl and H. K. Urbantke, Relativity, Groups, Particles, Springer, Wien (2001).

Thanks. I saw the table of contents of it and for me to understand that I imagine would be quite a struggle mathematically. Not that I'm not capable of understanding the math, but I find it hard (unfortunately) to enjoy studying mathematics without it having any physical meaning.

But I understand that such questions are like uhm .. trying to build a scyscraper starting at the 100th floor or trying to learn to swim immediately in the middle of the ocean.

I hope one day I will find it enjoyable to learn the nessecary mathematics though.

 

[PeroK]

I hope one day I will find it enjoyable to learn the nessecary mathematics though.

Whoever then has the effrontery to study physics while neglecting mathematics must know from the start that he will never make his entry through the portals of wisdom.

Roger Bacon (1214-84)

 

[vanhees71]

Thanks. I saw the table of contents of it and for me to understand that I imagine would be quite a struggle mathematically. Not that I'm not capable of understanding the math, but I find it hard (unfortunately) to enjoy studying mathematics without it having any physical meaning.

But I understand that such questions are like uhm .. trying to build a scyscraper starting at the 100th floor or trying to learn to swim immediately in the middle of the ocean.

I hope one day I will find it enjoyable to learn the nessecary mathematics though.

Then you have no chance to understand what has been figured out about your questions. This math is the only way to describe the physics and thus has fundamental physical meaning.