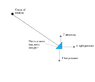
The discussion focuses on understanding the forces at play in a dynamic system involving balls and springs, particularly the force that prevents the system from rotating. Participants question the existence of a force that cancels out the radial force (FR) and explore whether the balls are pressing against a circular wall due to spring compression. It is clarified that pressure forces cannot produce net torque in a liquid, as they exert equal force on the enclosing boundary, resulting in a net force of zero. The conversation also highlights that torque arises from the springs rather than pressure, and that the attraction forces from the springs can indeed create torque on the balls. Overall, the complexity of the system and the interactions between forces are emphasized, with suggestions to simplify the scenario for better understanding.