F=ma for extended objects and movement of CM

[mfactor]

OK, so for a small particle, \Sigma F=mais very straight forward. If two forces are applied to that particle, the particle accelerates, which is determined by the summation of the forces applied.


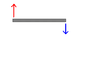
But what if the object is extended one, say, a solid uniform rod (1 kg). Also, imagine that I applied 6N on the left end and 5N on the right end, perpendicular to the rod, in opposite directions. (see attached picture).

What would be the resulting linear acceleration of the center of mass? Shouldn't F=ma still be applicable for center of mass only?
(Obviously torque is involved in this case also, but should it affect the linear accleration of the CM?)

how about an arbitrary portion of the rod (not center of mass)?


Picture: The red arrow up is 6N. The blue arrow down is 5N. The grey stick is the solid rod.

 

[Doc Al]

The sum of the forces will determine, via Newton's 2nd law, the linear acceleration of the rod's center of mass. Similarly, the sum of the torques will determine the rod's angular acceleration about its center of mass. The motion of an arbitrary point on the rod will be a combination of both motions.

 

[Farsight]

Is this one of those simple trick questions? I'm thinking that if I put 5N weight on the end of the rod and yank it up by the other end with 6N, it straightens out vertical, and it's like I'm pulling with 1N.

 

[BobG]

Is this one of those simple trick questions? I'm thinking that if I put 5N weight on the end of the rod and yank it up by the other end with 6N, it straightens out vertical, and it's like I'm pulling with 1N.

No.

For one thing, you're assuming the forces are inertial - they point the same direction regardless of the orientation of the rod. The problem doesn't say one way or the other.

If the forces are always perpendicular to the rod, you have 1N of Force causing the center of mass to accelerate. You have 11N * (whatever the distance between the center of mass and the ends) worth of torque causing rotational acceleration.

If the forces are inertial, you have a moving pendulum. The center of mass accelerates due to the 1N force and the rod swings back and forth forever (theoretically, if those are the only two forces that act on the rod).