- #1
ainster31
- 158
- 1
Homework Statement
Question + attempt:
Homework Equations
The Attempt at a Solution
Why is it that when I expand the factored form, I don't get the original equation?
You get m2 + (3/2)m + 1 = 0, which is equivalent to the original equation. Just multiply both sides by 2.ainster31 said:Homework Statement
Question + attempt:
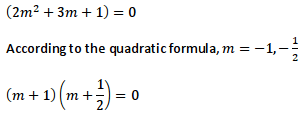
Homework Equations
The Attempt at a Solution
Why is it that when I expand the factored form, I don't get the original equation?
Mark44 said:You get m2 + (3/2)m + 1 = 0, which is equivalent to the original equation. Just multiply both sides by 2.
No. The Quadratic Formula requires that your equation be in the form ax2 + bx + c = 0, with a ≠ 0.ainster31 said:Let's say we have $$2{ m }^{ 2 }+3m+1=60$$.
Would I be able to apply the quadratic formula to the left hand-side of the equation only?
ainster31 said:How true is the below?

Mark44 said:What do you think? These look like textbook problems. Our policy here is that we don't do the work for students. Tell me what you think and why, and I'll tell you if you're right or where you went wrong.
The general form of a quadratic function is y = ax2 + bx + c. The right side of this can be written as a(x -r)(x -s). It's possible that r and s are complex numbers, though.ainster31 said:They're not problems. They're statements that I wrote.
If I recall correctly, in the 10th grade, the teacher said the general form of a quadratic equation is ##y=(x-r)(x-s)## and in the 11th grade, the teacher said the general form of a cubic equation is ##y=(x-r)(x-s)(x-t)##.
The general form of a cubic function is y = ax3 + bx2 + cx + d. The right side can be written in factored form as a(x - r)(x - s)(x - t), with possibly some of the roots being complex. Complex roots come in pairs, so we can't have more than two complex roots in a cubic equation.ainster31 said:However, in the 11th grade, the teacher changed it to ##y=a(x-r)(x-s)(x-t)## later.
Mark44 said:Note that 2(m + 1)(m + 1/2) = 0 and (m + 1)(m + 1/2) = 0 are equivalent equations. They both have exactly the same solutions.
Factoring a quadratic equation is the process of breaking down a quadratic equation into its factors, or expressions that can be multiplied together to get the original equation. This is done to solve the equation and find the values of x that make the equation true.
Some common mistakes include not properly identifying the type of quadratic equation (standard form, vertex form, etc.), not using the correct factoring method (e.g. difference of squares, grouping, etc.), and not checking the factored expression for accuracy.
To avoid mistakes, it is important to first identify the type of quadratic equation and then use the correct factoring method. It is also helpful to double check your work and make sure the factored expression satisfies the original equation.
One tip is to look for common factors first and then use the appropriate factoring method for the remaining expression. Another tip is to practice factoring frequently so that it becomes easier to recognize patterns and apply the correct methods.
Factoring can be used to solve a quadratic equation by setting the factored expression equal to zero and then solving for the values of x that make the expression equal to zero. These values will be the solutions to the original quadratic equation.