Feynman diagram for sigma+ -> n + pi+

makehhh
Messages
2
Reaction score
0

Homework Statement



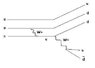
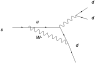
Hello, I am trying to draw a Feynman Diagram at quark level for the decay sigma+ -> neutron + pi+.

Homework Equations



sigma+ -> neutron + pi+
uus -> udd + udbar

The Attempt at a Solution



Well, the attachment is what I came up with. I have no idea if it's right to be honest, I can't see anything wrong with it, but I have no idea how to be methodical about these kinds of drawings, and haven't found any particle physics texts to be much help.

Thanks for your help!
 

Attachments

  • sigma+ to proton pi+.JPG
    sigma+ to proton pi+.JPG
    5.4 KB · Views: 1,711
Last edited:
Physics news on Phys.org
Well I can't see your diagram yet, but I think the diagram requires both a W- boson and a Z boson in it.
 
Last edited:
At least a W- and then a Z or a gamma.
 
So I think your diagram looks OK, but maybe someone else would like to confirm it.
 
My alternative was:
 

Attachments

  • feynman.png
    feynman.png
    954 bytes · Views: 927
Ah, yes that looks good, thanks for your help guys, much appreciated.
 

Thread 'Direction of the magnetic field of an oscillating charge'

Hello everyone, I’m considering a point charge q that oscillates harmonically about the origin along the z-axis, e.g. $$z_{q}(t)= A\sin(wt)$$ In a strongly simplified / quasi-instantaneous approximation I ignore retardation and take the electric field at the position ##r=(x,y,z)## simply to be the “Coulomb field at the charge’s instantaneous position”: $$E(r,t)=\frac{q}{4\pi\varepsilon_{0}}\frac{r-r_{q}(t)}{||r-r_{q}(t)||^{3}}$$ with $$r_{q}(t)=(0,0,z_{q}(t))$$ (I’m aware this isn’t...
View full post »

Thread 'Initial conditions for orbits around a wormhole'

Hi, I had an exam and I completely messed up a problem. Especially one part which was necessary for the rest of the problem. Basically, I have a wormhole metric: $$(ds)^2 = -(dt)^2 + (dr)^2 + (r^2 + b^2)( (d\theta)^2 + sin^2 \theta (d\phi)^2 )$$ Where ##b=1## with an orbit only in the equatorial plane. We also know from the question that the orbit must satisfy this relationship: $$\varepsilon = \frac{1}{2} (\frac{dr}{d\tau})^2 + V_{eff}(r)$$ Ultimately, I was tasked to find the initial...
View full post »

Similar threads

Amplitude of Feynman diagram in ##\phi^4## interactions
Replies
2
Views
3K
Feynman diagram; ##\pi^0+\pi^0\rightarrow \pi^++\pi^-##
Replies
1
Views
4K
Drawing the quark flow diagram for proton-pion interaction
Replies
3
Views
6K
How Do You Draw a Feynman Diagram for Pi-0 Decay?
Replies
1
Views
4K
Feynman Diagram Help: Decay of ∆+ to n + π+
Replies
3
Views
2K
Feynman Diagram: Simga+ -> p + gamma?
Replies
3
Views
2K
Feynman Diagrams for Interacting Scalar Fields
Replies
2
Views
3K
What is the Feynman diagram for Higgs decay to Z and gamma particles?
Replies
1
Views
3K
How Do You Draw Feynman Diagrams for These Particle Reactions?
Replies
14
Views
9K
Feynman Diagram of Neutron-Antineutron reaction
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top