Figuring this circuit's amp before resistor one

[StevenTorman]

< Mentor Note -- thread moved to HH from the technical forums, so no HH Template is shown >[/color]

https://drive.google.com/file/d/0B3gxtQyBRFkLQU9YdExMaTczTEk/view?usp=docslist_api

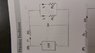
Here is the copy of the circuit I am try to anaylze.

I come up with three amps, but the answer book says .75 amps.

And now I am starting to think the book is wrong because I need to know the total resistance of the circuit.

Is there any help here?

 

[StevenTorman]

This is the pic that didn't load earlier

 

[Jony130]

The book answer is good, your answer is wrong. So please show as you work.
What is the voltage across 4 Ohm's resistor ??

 

[StevenTorman]

https://drive.google.com/file/d/0B3gxtQyBRFkLZEstUGQycm5pQVk/view?usp=docslist_api

Across the resistor, 3amps/4 ohms = .75

I see now, but I thought that amps across the circuit was measured based on total resistance. Therefore you must know all resistance.

Thus the .75 amps (and i measured voltage across the resistor, thus making the .75 a voltage calculation, not am amps calculation, correct?) would not be true if we knew the other two resistance?

Thanks for the help.

 

[Jony130]

Across the resistor, 3amps/4 ohms = .75

3 amps ?? how can amps divided by ohms give you amps on the result ??
Current is measured in Amperes. And voltage measured in volt. And in any circuit only amperes can flow. The voltage do not flow in the circuit.

I see now, but I thought that amps across the circuit was measured based on total resistance. Therefore you must know all resistance.

Please do not mix the voltage with the amperes.

Thus the .75 amps would not be true if we knew the other two resistance?

The answer will be true as long as total resistance for R2 and R3 is equal to:
R2||R3 = (R2 * R3)/(R2 + R3) = 9V/0.75A = 12Ω
So for example if R2 and R3 has any of this value 18Ω , 20Ω , 24Ω , 30Ω, 36Ω the solution given by the book is true.

 

[StevenTorman]

Johnny130, could you please show me where the three comes from then if it is not 3 amps.

All I did was take voltage Vsource12, the resistance R1:4 and divide them to get amps of 3.

You then indicated that I need to measure voltage across the resistor. This taking R1:4 and dividing by my derived amps 3. 4/3 = .75. This is what the book indicates at the answer 0.75I.

But as I think about the terms of measuring voltage across the intial resistor, it does not make sense in.

Any insight? (Please be patient, I am a novice)

 

[nsaspook]

You have an easily calculated voltage drop across the 4 ohm resistor with what's given on the diagram, 12 volts - 9 volts = 3 volts of voltage drop.
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/ohmlaw.html

 

[Jony130]

First of all; 1V = 1A * 1Ω, So amps times ohms give as voltage.
1A = 1V/1Ω Voltage divide by resistance gives us result in amperes.
So when you divided 3A/4Ω such division makes no sense.
As for the voltage across R1 resistor: The left part of a resistor is connected directly to 12V and the right leg of a resistor is connected to the node whose voltage is known to us and equal to 9V. So the voltage across R1 resistor is equal to VR1 = 12V - 9V = 3V and the current is I = 3V/4Ω = 0.75A.