Final electric potential difference in a circuit with two capacitors

[greg_rack]

Homework Statement

FIGURE ATTACHED BELOW
$C_{1}=2.00\mu F, q_{1}=6.00\mu C, C_{2}=8.00\mu F, q_{2}=12.0\mu C$
The circuit gets closed and charge flows until the two capacitors have the same electric potential difference $V_{F}$ across its terminals.
-calculate $V_{F}$.

Relevant Equations

$q=CV$

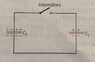
So, each capacitor must have a different potential difference, given by its capacity and charge... this would cause charge and current accordingly to flow in the circuit.
But how do I determine the final potential difference, which would of course be the same for both of them? I have tried writing down something, which I've found out to be unuseful to solve this problem.

 

[gneill]

The capacitors start out with different potentials across them. What are they?

If some amount of charge, say $\Delta q$ moves from the higher potential capacitor to the lower potential one, what expressions can you write for those new potentials?

 

[greg_rack]

The capacitors start out with different potentials across them. What are they?

If some amount of charge, say $\Delta q$ moves from the higher potential capacitor to the lower potential one, what expressions can you write for those new potentials?

Ok, so, since $V_{1}>V_{2}$, I'll have a $\Delta q$ transferring from 1 to 2, so the final potential $V_{f}$ is going to be: $V_{1f}=V_{2f}=V_{f}=\frac{q_{1}-\Delta q}{C_{1}}$... that makes sense, right?

 

[gneill]

Ok, so, since $V_{1}>V_{2}$, I'll have a $\Delta q$ transferring from 1 to 2, so the final potential $V_{f}$ is going to be: $V_{1f}=V_{2f}=V_{f}=\frac{q_{1}-\Delta q}{C_{1}}$... that makes sense, right?

Yes. But you're left with two unknowns: $V_f$ and $\Delta q$. Write the expressions for both of the capacitors and you'll have two equations in those two unknowns.

 

[greg_rack]

Yes. But you're left with two unknowns: $V_f$ and $\Delta q$. Write the expressions for both of the capacitors and you'll have two equations in those two unknowns.

Yep, sure!
Thank you very much :)