paulmdrdo1
- 382
- 0
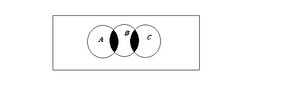
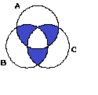
Find a Venn diagram containing three sets A, B, C such that $A\cap B\,\neq\,\emptyset$, $B\cap C\,\neq\,\emptyset$,and $C\cap A\,\neq\,\emptyset$, but $A\cap B\cap C\,=\,\emptyset$.
here's my answer please check if it is right.
View attachment 1127
here's my answer please check if it is right.
View attachment 1127