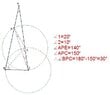
SUMMARY
In triangle ABC, with angles ACB and ABC both measuring 80 degrees, point P lies on segment AB such that BC equals AP. The objective is to determine the measure of angle BPC. The discussion highlights various approaches, including trigonometric and geometric proofs, with participants sharing insights and corrections regarding the proposed solutions. Notably, the 80-80-20 triangle is recognized for its rich structure and numerous problem-solving opportunities.
PREREQUISITES
- Understanding of triangle properties, specifically isosceles triangles.
- Familiarity with geometric constructions and proofs.
- Basic knowledge of trigonometric functions and their applications in geometry.
- Ability to interpret and analyze geometric diagrams.
NEXT STEPS
- Explore geometric constructions related to isosceles triangles, particularly the 80-80-20 triangle.
- Study trigonometric proofs in geometry, focusing on angle relationships.
- Investigate various methods for proving angle measures in triangle configurations.
- Review online resources that compile multiple solutions to geometric problems.
USEFUL FOR
Mathematicians, geometry enthusiasts, and students seeking to deepen their understanding of triangle properties and proof techniques.