Find charge due to two particles

[StephenDoty]

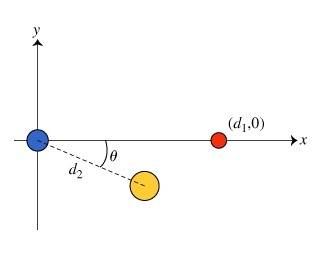
Suppose that the magnitude of the charge on the yellow sphere is determined to be 2q and at (d2cos(theta), -d2cos(theta). Calculate the charge q_red on the red sphere at (d1,0) with a positive blue sphere,q, at the origin and whose net force,F, is in the direction of -y. The yellow sphere is negative and the red sphere is positive. ( See picture bellow)
Express your answer in terms of q, d1,d2, and theta.

Well the Fx on blue due to the yellow sphere= k(2q)(q)/(d2cos(theta))^2
and the Fx on blue due to the red sphere = - k(q_red)(q)/(d1)^2

Now what? I am unsure as to what to do now. Any help would be appreciated.

Thank you.
Stephen

 

[StephenDoty]

Would you set them equal to each other?

 

[nova-ex]

I would? because of the fact that there is no net force along the x axis. Hence all x components of the force must cancel out to equal 0. Do you not get the right answer by doing that?

 

[StephenDoty]

I set them equal to each other and solved for q_red and got:

q_red= 2qd1^2/(d2^2)(cos(theta)^2)

Did I set up the original equations correctly? And did I find q_red correctly in terms of q, d1,d2, and theta?

Thank you. I really appreciate the help.

Stephen

 

[StephenDoty]

I have to turn this in soon so any help would be appreciated.

thank you.

Stephen

 

[nova-ex]

I don't see anything wrong with it. Does anyone else see anything wrong with it?

 

[StephenDoty]

bump
Does everyone agree with nova-ex? Are my equations correct?

 

[StephenDoty]

Not to be a bother but I have to turn this in tomorrow. So if you can please tell me whether or not I set the problem up correctly and got the correct formula for q_red: q_red= 2qd1^2/[(d2cos(theta))^2]?

Thanks I would really appreciate it.

Stephen

 

[StephenDoty]

Any opinions?