PFuser1232
- 479
- 20
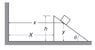
Suppose we want to find the constraint equation relating the acceleration of a block on a wedge to the acceleration of the wedge (see attached images). We can write:
$$h - y = (x - X) \tan{\theta}$$
What if ##X## was measured to the centre of mass of the wedge for instance? Wouldn't the correct equation be:
$$h - y = (X - x) \tan{\theta}$$
$$h - y = (x - X) \tan{\theta}$$
What if ##X## was measured to the centre of mass of the wedge for instance? Wouldn't the correct equation be:
$$h - y = (X - x) \tan{\theta}$$