npellegrino
- 17
- 0
I am having difficulty figuring this one, any guidance will be appreciated.
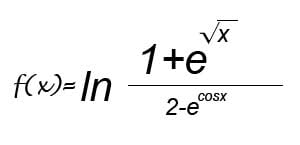
I believe i use this rule d/dx log a ^ u = 1/(lna)u
now i need to take the derivative of u, does e^sqrtX = e^sqrtX or is it e^sqrtX * derivative of sqrtX making it e^sqrtX * 1/2sqrtX