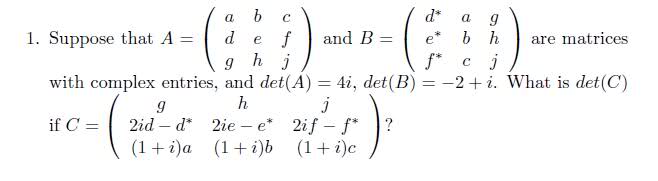Find Det (C) knowing Det(A) and Det(B)

[mmmboh]

Hi, right now I have two 3x3 matrices with letter entries, I know the determinant of A and the determinant of B, and I am given a matrix C for which I have to find the determinant for. Right now I am expressing matrix C as a combination of A and B, but what happens to the determinant when I add matrices A and B together?

 

[Dick]

One of the rows of C is a linear combination of two vectors. det is linear in the row entries, right?

 

[mmmboh]

Well all the rows in C are a linear combination of vectors in A and B.

 

[Dick]

Well all the rows in C are a linear combination of vectors in A and B.

I'm referring to the second row being a sum of two vectors.

 

[mmmboh]

Ok, that's true, but how does that help me in finding the new determinant? I still have to know what happens when I add the matrices together, unless you mean something else?

 

[Dick]

I mean that if the letters A, B, C, and D are row vectors then det(A,B+D,C)=det(A,B,C)+det(A,D,C). det is linear in the row vectors.

 

[mmmboh]

Ah I didn't know you can do that :S...thanks!

 

[mmmboh]

But wait I don't understand how that works...why do the B and D add but nothing else...isn't this sort of like saying det(A+B)=det(A)+det(B) which isn't true?

 

[Dick]

But wait I don't understand how that works...why do the B and D add but nothing else...isn't this sort of like saying det(A+B)=det(A)+det(B) which isn't true?

No, it's not the same thing. I'm using that det is a multilinear function of it's rows (or columns). It's a fundamental property of the determinant. Try and find it in your book. It's important.