Find distance electron travels before turning around

[penguinnnnnx5]

Homework Statement

The hydrogen molecular ion H1,2, with one electron and two protons, is the simplest molecule. The equilibrium spacing between the protons is 0.11 nm. Suppose the electron is at the midpoint between the protons and moving at 1.5 * 10^6 m/s perpendicular to a line between the protons.

How far (in nm) does the electron move before reaching a turning point? Because of their larger mass, the protons remain fixed during this interval of time.

Homework Equations

PE = kQq/r
KE = 1/2 mv²
W = KE + PE
k = 9*10⁹

The Attempt at a Solution

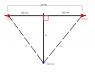
I first drew a diagram to get an idea of how to approach this problem.

Let x² = .055 nm

R = √(D² + x²)

-ΔKE = ΔPE
-(-KE_i) = PE_f

1/2 mv² = kQq/R + kQq/R = 2kQq/R

R = 4kQq/(mv²) = √(D² + x²)

D² + x² = [4kQq/(mv²)]²

D = √( [4kQq/(mv²)]² - x² )

D = ~.447 nm

This answer, however, is wrong. The correct answer is 3.0 * 10^-3 nm.

I tried integrating from F, but I still found the same equation for PE. Am I doing something incorrect? Please help as I need to know this by tomorrow for my midterm. Thank you for any help received!

 

[penguinnnnnx5]

So the KE = -PE method is correct? If it is, then I'm not sure what I'm doing wrong at all.

The final answer I have does not match up to the correct answer. It's even off by a factor of ten.

 

[ehild]

PE+KE = const. The potential energy is not zero at the midpoint. Change of potential energy= final KE.

ehild

 

[penguinnnnnx5]

So the set-up should be

PEf - PEi = KEf

2KQq (1/R - 1/x) = 1/2 mv^2 ?

 

[voko]

What is x² and why is it 0.055 nm?

 

[ehild]

So the set-up should be

PEf - PEi = KEf

2KQq (1/R - 1/x) = 1/2 mv^2 ?

yes.

ehild

 

[penguinnnnnx5]

What is x² and why is it 0.055 nm?

x is just a value I used to clean up the work before plugging everything in.

The problem states that the electron travels in the path of a perpendicular bisector of an imaginary line connecting the two protons. If you were to find the radius of that, then it'd be half of the length of the line squared plus the distance traveled squared under a radical. Rather than saying Sqrt( L^2/4 + D^2), it seemed cleaner to say Sqrt( x^2 + D^2) and make x = (1/2)L, L being the length of the line connecting the two protons.

 

[penguinnnnnx5]

yes.

ehild

So I have something like this:

2kQq(1/R - 1/x) = 1/2 mv²

(x-R)/(xR) = (mv²)/(4kQ²) <--- because Q=q=1.6*10^-19

(xR)/(x-R) = (4kQ²)/(mv²)

mv²xR = 4kQ²x - 4kQ²R

(mv²x + 4kQ²)R = 4kQ²

R = (4kQ²)/(mv²x+4kQ²)

√(x²+D²) = (4kQ²)/(mv²x+4kQ²)

D² = (4kQ²)/(mv²x+4kQ²)² - x²

D = √[(4kQ²)/(mv²x+4kQ²)² - x²]

However, when I plug in all the values:
x = .055 * 10^-9 m
Q = 1.6 * 10^-19 C
m = 9.1 * 10^-31 kg
v = 1.5 * 10⁶ m/s

I get the square root of a negative number.

Edit:

The set up is supposed to be

KEi = PEi - PEfBUT it should look like this:

-2kQq(1/R-1/x) = 1/2 mv²

2kQq(1/x-1/R) = 1/2 mv² because Q (the source charges) is 1.6 * 10^-19 while q = -1.6 * 10^-19

(R-x)/(xR) = (mv²)/(4kQ²)

(xR)/(R-x) = (4kQ²)/(mv²)

mv²xR = 4kQ²R - 4kQ²x

(mv²x - 4kQ²)R = 4kQ²

R = (4kQ²)/(mv²x-4kQ²)

√(x²+D²) = (4kQ²)/(mv²x-4kQ²)

D² = (4kQ²)/(mv²x-4kQ²)² - x²

D = √[(4kQ²)/(mv²x-4kQ²)² - x²]

Plug everything in, and you should be able to get 3.00131072 * 10^-2 nm

 

[voko]

x is just a value I used to clean up the work before plugging everything in.

The problem states that the electron travels in the path of a perpendicular bisector of an imaginary line connecting the two protons. If you were to find the radius of that, then it'd be half of the length of the line squared plus the distance traveled squared under a radical. Rather than saying Sqrt( L^2/4 + D^2), it seemed cleaner to say Sqrt( x^2 + D^2) and make x = (1/2)L, L being the length of the line connecting the two protons.

But why is its SQUARE equal to 0.055 nm?

 

[penguinnnnnx5]

But why is its SQUARE equal to 0.055 nm?

Oh, I'm sorry. That was a typo in the introduction of the problem. It is supposed to be x = .055 nm.

I have not been using the wrong value for x or x² though, so I am still a little lost.

Edit:

Refer to my previous post as the answer and work is in that post.

 

[voko]

because Q=q=1.6*10^-19

Is that really so?

 

[ehild]

So I have something like this:

2kQq(1/R - 1/x) = 1/2 mv²

It is
2kQq(1/x - 1/R) = 1/2 mv, as KE(initial)=PE(final)-PE(initial). But qQ is a negative number, so your equation is correct if you use the absolute value for the electron charge.

Previously you called the vertical displacement "x". It is better to denote the distance from a proton by "d", for example.

Do not complicate the calculations. Plug in the data, calculate 1/R-1/x. Do not round too much.
(1/R-1/x) can be also written as 1/R(1-R/x).

ehild

 

[penguinnnnnx5]

It is
2kQq(1/x - 1/R) = 1/2 mv, as KE(initial)=PE(final)-PE(initial). But qQ is a negative number, so your equation is correct if you use the absolute value for the electron charge.

Previously you called the vertical displacement "x". It is better to denote the distance from a proton by "d", for example.

Do not complicate the calculations. Plug in the data, calculate 1/R-1/x. Do not round too much.
(1/R-1/x) can be also written as 1/R(1-R/x).

ehild

Thank you. As you see above, I found the correct answer. "x" was not set as the vertical displacement, however. Instead, I set "x" as half of the length of the line connecting the two protons and "D" as the distance from the midpoint of the referred line.

I also now see why it is (1/x - 1/R) due to your explanation. As always, you seem to have fully answered my questions without giving away the answers, allowing me to figure out the entire problem. Thank you so much for all the times you have helped me, ehild! :)

 

[penguinnnnnx5]

Is that really so?

That was my greatest error, as ehild also pointed out. Thank you for your time and effort in helping me understand this problem!

 

[ehild]

Well, sorry, I forgot your notations. The PE(final)-PE(initial)=2kqQ(1/R-1/x) , your equation was correct. But q is negative.
Have you got 0.003 nm really? I could not get the same result...

ehild

 

[penguinnnnnx5]

Well, sorry, I forgot your notations. The PE(final)-PE(initial)=2kqQ(1/R-1/x) , your equation was correct. But q is negative.
Have you got 0.003 nm really? I could not get the same result...

ehild

Yes I have!
Like you said, since q is negative, the (1/R-1/x) becomes (1/x-1/R) instead.
So,

PE_f - PE_i = 1/2 mv²

2kQq(1/R-1/x) = 1/2 mv²

-2kQ²(1/R-1/x) = 1/2 mv² Since q = -Q

2kQ²(1/x-1/R) = 1/2 mv²

1/x - 1/R = (mv²)/(4kQ²)

(R-x)/xR = (mv²)/(4kQ²)

xR/(R-x) = (4kQ²)/(mv²)

(mv²) xR = (4kQ²)R - (4kQ²)x

[(mv²)x - (4kQ²)]R = -(4kQ²)x

R = -(4kQ²)x/[(mv²)x - (4kQ²)]

Since R = √(x²+D²)

√(x²+D²) = -(4kQ²)x/[(mv²)x - (4kQ²)]

x²+D² = [ -(4kQ²)x/[(mv²)x - (4kQ²)] ]²

D² = [ -(4kQ²)x/[(mv²)x - (4kQ²)] ]² - x²

D = √ ( [ -(4kQ²)x/[(mv²)x - (4kQ²)] ]² - x² )

With this equation, I found .003 nm. This was after multiplying the result with 10⁹ so convert from meters to nanometers, of course.

 

[ehild]

OK, I have found my mistake...


KE=(-2kqQ/x)(1-x/R)
So KE=1.0248˙10^-18
-2kgQ/x=8.388˙10^-18
1-x/R=0.1222...

ehild