Thanks for fast response chiro
After I posted this I searched this forum for related issues and got some answers which is close to your answer. However, when I apply it I don't get feasible results.Assuming P4 as the point to find, similar to plane eqn you mention it, I used, a norm vector as
N=cross(P2-P1,P2-P3), where cross is cross product
then normalize it,
N/norm(N).
dot(P4-P2,N)=0 ...(1) where dot means dot product.
and got the plane equation. Having length d,
norm(P4-P2)=d ...(2)
which will contain sequared variables. Also, I have
dot(P4-P2,P4-P1)=0...(3)
cause the line P4P1 should be normal to P4P2, and ths equation will contains sequared variables. Subtracting eqn (2) from (3) I will get a second linear equation.
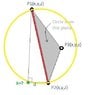
Any point on the sphere will be true, so my point P4 is applied to the sphere equation which need (Pc) center of sphere and its radius (r).
Pc=(P1+P2)/2 and r=norm(P1-Pc), correct?
so,
norm(Pc-P4)=r ...(4)
which will contains squared variables. Subtracting (4) from (2) will get the third linear equation. Solving the 3 linear equations to get P4(x,y,z) gave not feasible answers.
May I get help on this please, did I have to normalize other vectors?, my background in vectors is not that much and all I knew learned from your forum. Any wrong in this procedure. Thanks in advance.