quee
- 7
- 2
Hello.
There is a problem:
"Through D on a side AB of the triangle ABC drawn a line parallel to AC intersecting BC in E. D is such that CD:DB = m:n. Find DE:AC"
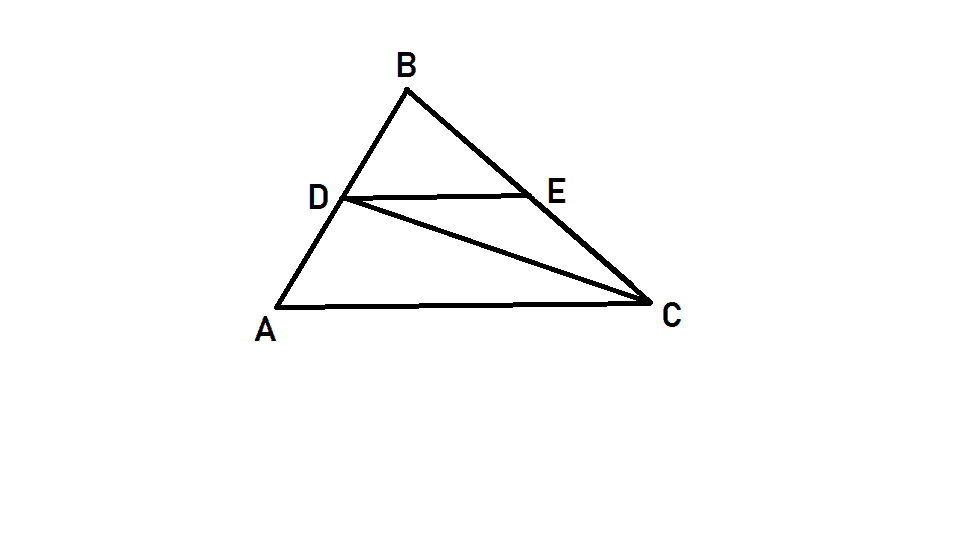
So it is easy to find out that DB:AB equals to DE:AC as DE and AC are parallel. Since DB = n, there is only one need to express AB in terms of n and m. But how to do it? I tried using similar triangles, but I can't get AB through it. The trapezoid ADEC also gives no results as the second diagonal is unknown.
There is a problem:
"Through D on a side AB of the triangle ABC drawn a line parallel to AC intersecting BC in E. D is such that CD:DB = m:n. Find DE:AC"
So it is easy to find out that DB:AB equals to DE:AC as DE and AC are parallel. Since DB = n, there is only one need to express AB in terms of n and m. But how to do it? I tried using similar triangles, but I can't get AB through it. The trapezoid ADEC also gives no results as the second diagonal is unknown.