- #1
solarcat
- 22
- 3
- Homework Statement
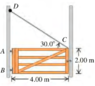
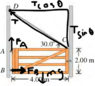
- A gate 4 m wide and 2 m high weights 700 newtons. It is hinged on the left side at two points, A and B (A is above B). A cord CD is connected at the other end of the gate across from A. The horizontal force at A is 0. I'm supposed to calculate the torque due to to the tension in the cord two different ways, using the lever arm of the force and the horizontal and vertical components of the tension.
- Relevant Equations
- Torque = Force*Distance
I thought that the upward/vertical torque due to the cord might be T*sin 30 deg * sqrt (4^2 + 2^2). Then this would have to equal the weight of the gate times the distance (700 N * 2 m). This gives a tension force of 626 Newtons but it's not the right answer. I don't even know what the lever arm of the force is or how to even use that to find tension.