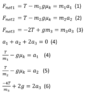Find the accelerations of all three blocks and the tension in the rope

[rashida564]

Homework Statement

In the system shown above m1 > m2 . The pulleys are massless and frictionless, and the
rope joining the blocks has no mass. The coefficient of static friction between the blocks
and the tables is greater than the coefficient of kinetic friction: µs > µk . The downward
acceleration of gravity is g .
Now consider the case where, when released from rest, all three blocks
begin to move. Find the accelerations of all three blocks and the tension in
the rope.

Relevant Equations

F=ma

I am thinking about solving it this way.
The first three equation is from Newton law.
Then the forth one is the constrain equation, after that I simplified the first three equations, and I am thinking about plugging them into the forth equation and solve for T after that I get the value of each acceleration, but I have 10% scared that I am having sign wrong in one of them.
Sorry about writing the equation as picture I want to improve my writing, but going to learn LaTex after exams.

 

[etotheipi]

I believe in order to be consistent with your first 3 equations, the fourth equation should read $a_{1} + a_{2} = 2a_{3}$, since all of the accelerations are taken to be positive. Either that or reverse the signs of the first two Newton II relations, to be consistent with the directions of $x_{1}$ and $x_{2}$ on your diagrams. It doesn't matter which you choose.

Then, the system has 4 equations and 4 unknowns so it should be possible to solve.

 

[rashida564]

Thanks mate, now I see my mistake.