- #1
beefiestcrib55
- 1
- 0
1. Homework Statement
The curve of y= 4/(x^2+4), the x-axis, and the vertical lines x = -2 and x = 2
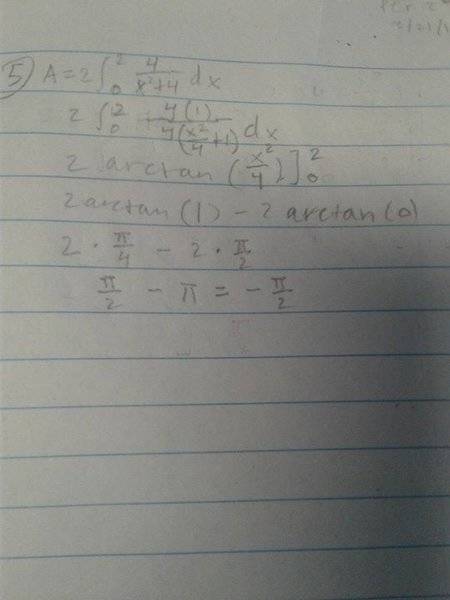
The curve of y= 4/(x^2+4), the x-axis, and the vertical lines x = -2 and x = 2

Math_QED said:##\int \frac{1}{x^2 + 1} dx = \arctan(x) + c##, not ##arctan(x^2)+c##
The formula for finding the area of a region given the boundaries is to subtract the lower boundary from the upper boundary and then multiply by the width of the region. This can be represented as A = (upper boundary - lower boundary) * width.
The boundaries of a region are typically given in the problem or can be identified from a graph or diagram. They can also be determined by finding the points where the graph intersects the x-axis or y-axis.
Yes, the boundaries of a region can be negative numbers. However, when using the formula to find the area, it is important to make sure that the upper boundary is larger than the lower boundary.
The units used for the width when finding the area of a region should match the units of the boundaries. For example, if the boundaries are given in meters, the width should also be in meters.
Yes, there are a few special cases when finding the area of a region. If the region is a rectangle, the formula is simply A = length * width. If the region is a triangle, the formula is A = 1/2 * base * height. Additionally, if the boundaries are curves, the area can be found using calculus.