Find the equivalent capacitance

Click For Summary

Homework Help Overview

The discussion revolves around finding the equivalent capacitance of a circuit involving multiple capacitors with given values and an applied voltage. The capacitors in question include two 8.0 microF capacitors and three 4.2 microF capacitors, with the total voltage applied across them being 230V.

Discussion Character

  • Exploratory, Assumption checking, Problem interpretation

Approaches and Questions Raised

  • Participants explore the configuration of capacitors, questioning which are in series or parallel. There are attempts to simplify the circuit by combining capacitors into equivalent capacitances, particularly focusing on C3 and C4 being in series.

Discussion Status

Participants are actively discussing the relationships between the capacitors, with some suggesting methods to reduce the circuit complexity. There is a recognition of the need to clarify the series and parallel connections, and some participants express confusion about voltage relationships in these configurations.

Contextual Notes

There is an ongoing discussion about the definitions of series and parallel connections, particularly in relation to voltage across capacitors. Some participants are unsure about the implications of junctions in the circuit affecting these classifications.

mathnoobie
Messages
62
Reaction score
0

Homework Statement



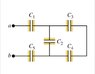
In the figure, C1 = C5 = 8.0 microF and C2 = C3 = C4 = 4.2 microF . The applied potential is Vab = 230V

Homework Equations


1/Ceq=1/C1+1/C2+...+1/Cn(for series connections)
Ceq=C1+C2+...+Cn



The Attempt at a Solution


The answer is 2.4x10^-6

So far I have tried to set C1 to C5 all in series, but that gives me the wrong solution.
I'm not sure what to do, could anyone hint me in the right direction?
 

Attachments

  • capa.JPG
    capa.JPG
    12.2 KB · Views: 2,143
Physics news on Phys.org
Two capacitors are in series, if they are connected, and nothing else is connected to the point where the two capacitors are connected.
5 capacitors would be in series if they were alll connected in a string and nothing else is connected to any point between the capacitors. C1 to C5 are obviously not in series.
There are however 2 capacitors that are in series. You can replace them with their equivalent capacitance and continue from there.
 
willem2 said:
Two capacitors are in series, if they are connected, and nothing else is connected to the point where the two capacitors are connected.
5 capacitors would be in series if they were alll connected in a string and nothing else is connected to any point between the capacitors. C1 to C5 are obviously not in series.
There are however 2 capacitors that are in series. You can replace them with their equivalent capacitance and continue from there.

C3 and C4 are in series, if I get their equivalent Capacitors, they would be in parallel with C2,
then C234 would be in series with C1 and C5?

edit: Yep, I got the answer, thank you :)
Quick question regarding series connections though.

The reason I was unable to say C1, C2, C5 were in series was because of the junction right?
 
Last edited:
willem2 said:
C1 to C5 are obviously not in series.

C1 and C5 are in series with each other on the path from a to b
willem2 said:
C3 and C4 are in series, if I get their equivalent Capacitors, they would be in parallel with C2,
then C234 would be in series with C1 and C5?

That looks correct to me
 
dinospamoni said:
C1 and C5 are in series with each other on the path from a to b

I am confused on what you mean by this, could you explain further if possible?
 
Just keep shrinking the circuit down by replacing individual capacitors with equivalence capacitors until you are down to a single Ceq. You can start by noticing that C3 and C4 are in series and replacing them with Ceq1. After doing this, you should notice that Ceq1 and C2 are in parallel, so you can replace them with Ceq2. After doing this, you should be left with 3 capacitors which are all in series.

It helps to redraw the circuit every time you replace capacitors with an equivalence capacitor.
 
Sure. With these problems, I like to find all possible paths from point a to point b.

In this case you can go from C1 to C2 to C5, or you can go from C1 to C3 to C4 to C5. Notice how C1 and C5 are in both paths. This means that you can't get from point a to point b without going through both C1 and C5, so they are in series.

Alternatively, C2 is in only the first while C3 and C4 are in only the second, so they are in parallel with each other. Note that C2 is only in parallel with BOTH C3 and C4 because they are in series with each other.

Does that help?
 
dinospamoni said:
Sure. With these problems, I like to find all possible paths from point a to point b.

In this case you can go from C1 to C2 to C5, or you can go from C1 to C3 to C4 to C5. Notice how C1 and C5 are in both paths. This means that you can't get from point a to point b without going through both C1 and C5, so they are in series.

Alternatively, C2 is in only the first while C3 and C4 are in only the second, so they are in parallel with each other. Note that C2 is only in parallel with BOTH C3 and C4 because they are in series with each other.

Does that help?

Yes greatly, you explained how to find series/parallel connections much better than my book, all my book said was if the charge is equal they are in series, if the voltage is equal they are in parallel.
 
dinospamoni said:
Sure. With these problems, I like to find all possible paths from point a to point b.

In this case you can go from C1 to C2 to C5, or you can go from C1 to C3 to C4 to C5. Notice how C1 and C5 are in both paths. This means that you can't get from point a to point b without going through both C1 and C5, so they are in series.

Alternatively, C2 is in only the first while C3 and C4 are in only the second, so they are in parallel with each other. Note that C2 is only in parallel with BOTH C3 and C4 because they are in series with each other.

Does that help?

Wait, how is C2 in parallel with C3 and C4 when their voltages don't equal (V2=V3=V4)
 
  • #10
mathnoobie said:
Wait, how is C2 in parallel with C3 and C4 when their voltages don't equal (V2=V3=V4)

I haven't calculated anything for voltage, but my guess would be because they shouldn't be equal.

I'd say the voltage across C2 must be equal to the voltage across 3 + across 4.

Voltage is opposite of capacitance:
In series:
Veq= V1 + V2 + ...

1/Ceq=1/C1+1/C2+...

In parallel:

1/Veq= 1/V1 + 1/V2 + ...

Ceq=C1+C2+...
 
  • #11
dinospamoni said:
I haven't calculated anything for voltage, but my guess would be because they shouldn't be equal.

I'd say the voltage across C2 must be equal to the voltage across 3 + across 4.

Voltage is opposite of capacitance:
In series:
Veq= V1 + V2 + ...

1/Ceq=1/C1+1/C2+...

In parallel:

1/Veq= 1/V1 + 1/V2 + ...

Ceq=C1+C2+...

They aren't equal, I calculated them. V1=V5, and V3=V4, V2=V3+V4.

dinospamoni said:
Note that C2 is only in parallel with BOTH C3 and C4 because they are in series with each other.
My question was though, how can we say that they are in parallel(C2, C3, C4) if their voltages do not equal. I am probably not interpreting your statement correctly.
 
  • #12
mathnoobie said:
They aren't equal, I calculated them. V1=V5, and V3=V4, V2=V3+V4.


My question was though, how can we say that they are in parallel(C2, C3, C4) if their voltages do not equal. I am probably not interpreting your statement correctly.

Ah ok good I'm glad you calculated them.

Think of it like this:

There is some Voltage at point A and at point B the voltage must equal zero (This is just in general for a circuit just to get the idea in your head). Now, if a charge makes it from point a to point b, it has lost all of its potential (voltage).

You can think of this the same way as before: identify all the paths current can travel.
Each path must decrease the voltage to zero.

You can go C1 to C2 to C5 OR you can go C1 to C3 to C4 to C5. Each path must bring the voltage to zero.

Since C1 and C5 are in both paths, they both bring down the voltage the same amount in both paths, so don't think about them for now.

This leaves just C2 for path 1 and C3 and C4 for path 2.

If both paths lower the voltage the same amount, V2 must equal V3 + V4

which is what you showed with your voltage calculations
 
  • #13
dinospamoni said:
Ah ok good I'm glad you calculated them.

Think of it like this:

There is some Voltage at point A and at point B the voltage must equal zero (This is just in general for a circuit just to get the idea in your head). Now, if a charge makes it from point a to point b, it has lost all of its potential (voltage).

You can think of this the same way as before: identify all the paths current can travel.
Each path must decrease the voltage to zero.

You can go C1 to C2 to C5 OR you can go C1 to C3 to C4 to C5. Each path must bring the voltage to zero.

Since C1 and C5 are in both paths, they both bring down the voltage the same amount in both paths, so don't think about them for now.

This leaves just C2 for path 1 and C3 and C4 for path 2.

If both paths lower the voltage the same amount, V2 must equal V3 + V4

which is what you showed with your voltage calculations

Ah, I never thought of using Kirchoff's loop law for some reason, but after you made the connection for me I understand what you mean. Thanks for taking the time to help me :)
 
  • #14
mathnoobie said:
Ah, I never thought of using Kirchoff's loop law for some reason, but after you made the connection for me I understand what you mean. Thanks for taking the time to help me :)

No problem. Glad I could help :)
 

Similar threads

Struggling to find the equivalent capacitance of this circuit
  • · Replies 11 ·
Replies
11
Views
3K
Equivalent Capacitance and Resistance of this Circuit
  • · Replies 27 ·
Replies
27
Views
5K
Equivalent Capacitance in a circuit
  • · Replies 7 ·
Replies
7
Views
2K
Find equivalent capacitance in a network with parallels and series
  • · Replies 1 ·
Replies
1
Views
3K
Equivalent Capacitance and Voltage Across
  • · Replies 19 ·
Replies
19
Views
2K
Find the equivalent capacitance of the circuit
  • · Replies 12 ·
Replies
12
Views
2K
Two-layer dielectric, four-capacitor model vs three-capacitor model
  • · Replies 5 ·
Replies
5
Views
1K
Calculate the equivalent capacitance in the network
  • · Replies 1 ·
Replies
1
Views
4K
Capacitance in a Complicated Mixed Circuit
  • · Replies 19 ·
Replies
19
Views
2K
What is the equivalent capacitance of this formation?
  • · Replies 8 ·
Replies
8
Views
2K