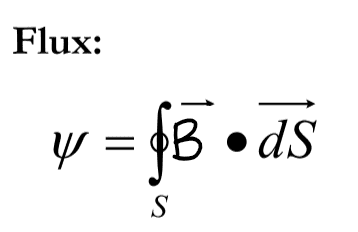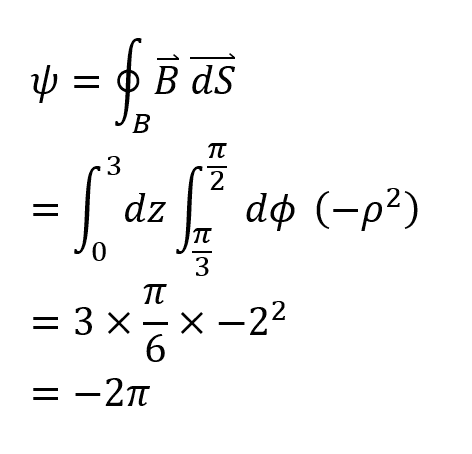SUMMARY
The discussion centers on calculating the flux due to a vector field crossing an open surface, specifically examining the vector field defined as ## \bf A = rz~ \hat {\bf \theta} ##. The participant asserts that the curl of this vector field, calculated as ## \nabla \times \bf A ##, results in ## (z/r)~ \hat {\bf k} - \hat {\bf r} ##, which contradicts an unspecified reference. This discrepancy raises questions about the fields involved and their definitions.
PREREQUISITES
- Understanding of vector calculus, specifically curl operations.
- Familiarity with cylindrical coordinates and their notation.
- Knowledge of vector fields and their physical interpretations.
- Basic principles of surface integrals in electromagnetism.
NEXT STEPS
- Review the properties of curl in vector calculus.
- Study cylindrical coordinate transformations and their applications.
- Explore the implications of vector fields in physics, particularly in electromagnetism.
- Investigate common errors in vector field calculations and their resolutions.
USEFUL FOR
Students and professionals in physics and engineering, particularly those focused on vector calculus, electromagnetism, and fluid dynamics.