Find the force which makes the box jump

[kaspis245]

Homework Statement

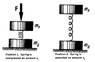
What force one need to push the box with mass $m_1$ for the box with mass $m_2$ to jump when the force disappears?

Homework Equations

Newton's second law.

The Attempt at a Solution

System, when the force is applied:

System, when the force disappears:

$F$ is the force, which is applied to the box. This force and $m_1g$ creates the spring force, namely $kx$. From the second system I can see, that the box with mass $m_2$ will jump only if $kx$ is greater than $m_2g$, therefore:

$F+m_1g=kx$
$kx=m_2g$$F=m_2g-m_1g=g(m_2-m_1)$

Is this correct?

 

[TSny]

Does your answer make sense for the case where $m_1$ = $m_2$?

When the force is removed, the top mass must move upward to a new position before the bottom mass leaves the floor. So, you need to distinguish between the value of x when F is released and the value of x when m₂ leaves the floor.

 

[Doc Al]

You might find it useful to ask yourself these questions:

- What force (magnitude and direction) does the spring exert on m2 before the force F is applied?
- What force (magnitude and direction) must the spring exert on m2 for m2 to be lifted off the ground?​

 

[kaspis245]

- What force (magnitude and direction) does the spring exert on m2 before the force F is applied?​

Before the force $F$ is applied the spring exert a force equal to $m_1g$.

- What force (magnitude and direction) must the spring exert on m2 for m2 to be lifted off the ground?

The spring must exert a force which is greater than $m_2g$.

I understand that my answer $F=g(m_2−m_1)$ doesn't make sense, but no matter what I do I come up with it every time.

Here's another try:

When the force $F$ is applied, mass $m_2$ is affected with a downward force of $m_2g+m_1g+F$ and an upward force of $F_N$. When the spring is released, it becomes stretched and compressed again. The spring force that pushes the boxes when the spring is stretching and the spring force that pulls the boxes when the spring is compressing is the same and equal to $m_1g+F$. So in order for the box with mass $m_2$ to jump the spring force must be at least equal to $m_2g$, therefore: $m_2g=m_1g+F$. Where is my reasoning wrong?

 

[TSny]

As mentioned earlier, after F is removed $m_1$ moves upward to a new position before $m_2$ leaves the floor. So the force of the spring at the instant $m_2$ leaves the ground is not the same as the force of the spring at the instant F is removed. Let $x_1$ be the amount the spring is compressed when F is removed and let $x_2$ be the amount the spring is stretched when $m_2$ leaves the floor. Try to see why $x_1 \neq x_2$.

 

[kaspis245]

I think I understand it now. This $x1≠x2$ applies, because when the spring is stretching, the force $m_1g$ opposes the motion. This follows, that the spring force which makes $m_2$ to jump is equal to $F$.

$F=m_2g$

Is that the answer?

 

[Doc Al]

Before the force $F$ is applied the spring exert a force equal to $m_1g$.

Right, but in what direction is the force?

The spring must exert a force which is greater than $m_2g$.

Again, in what direction?

In order to have the spring force change as it needs to, how much must the spring be stretched above the equilibrium point?

 

[TSny]

I think I understand it now. This $x1≠x2$ applies, because when the spring is stretching, the force $m_1g$ opposes the motion. This follows, that the spring force which makes $m_2$ to jump is equal to $F$.

$F=m_2g$

Is that the answer?

I don't believe that is the right answer. How did you conclude that the spring force which makes $m_2$ jump is equal to $F$?

 

[kaspis245]

Now I'm completely confused. I'll try to explain it one more time:

(1) When the downward force $F$ is applied, the spring exerts an upward force $m_1g+F$.

(2) When $F$ is removed, the spring causes $m_1$ to move upwards with a force $m_1g+F$.

(3) Since $m_1g$ opposes the motion, the spring will be stretched with a force $(m_1g+F)-m_1g=F$.

(4) Then, the string becomes compressed with the sum of downward forces $F+m_1g$ and since this compressed string must exert a force which is greater than $m_2g$, I am left with the same $F=g(m_2−m_1)$...

I've given each statement a number. Please tell me which of these statements are incorrect.

 

[Doc Al]

(1) When the downward force $F$ is applied, the spring exerts an upward force $m_1g+F$.

Can't argue with that one!

(2) When $F$ is removed, the spring causes $m_1$ to move upwards with a force $m_1g+F$.

Not quite sure what you mean. The spring still exerts the upward force $m_1g+F$.

(3) Since $m_1g$ opposes the motion, the spring will be stretched with a force $(m_1g+F)-m_1g=F$.

Not sure what you mean by "stretched by". When $F$ is removed, there is a net force of $F$ acting upward on $m_1$.

(4) Then, the string becomes compressed with the sum of downward forces $F+m_1g$ and since this compressed string must exert a force which is greater than $m_2g$, I am left with the same $F=g(m_2−m_1)$...

This confuses me. For one thing, the spring had better be stretched, not compressed, in order to lift $m_2$.

Try this. Using your own example, once the force is removed and the mass reaches its highest point, what will the force be on $m_2$? (That's what you need to set equal to $m_2 g$.)

 

[kaspis245]

I see, so the fourth statement is incorrect (sorry for the mistakes, English is not my native language).

$m_1$ at it's highest point is affected by two downward forces: $m_1g$ and $F$ (caused by the string). At the same moment, $m_2$ will be affected by an upward spring force $F$ and downward force $m_2g$. Therefore, in order for $m_2$ to jump: $F=m_2g$. I really hope you are not irritated with me.

 

[TSny]

$m_1$ at it's highest point is affected by two downward forces: $m_1g$ and $F$ (caused by the string). At the same moment, $m_2$ will be affected by an upward spring force $F$ and downward force $m_2g$. Therefore, in order for $m_2$ to jump: $F=m_2g$.

Yes, that sounds right.

It gets confusing if you use the same symbol $F$ for different things. It would be best to let $F$ stand for the unknown force that held $m_1$ down before it was released. $F$ is the unknown. If you want to refer to the force of the spring at the starting point, then maybe use $f_{sp, 1}$ and for the final point where $m_2$ starts to leave the floor the spring force would be $f_{sp, 2}$.

 

[Doc Al]

$m_1$ at it's highest point is affected by two downward forces: $m_1g$ and $F$ (caused by the string).

As TSny just pointed out, do not confuse the force applied to the mass ($F$) with the force produced by the spring.

For some reason, you never seem to answer my questions.

 

[kaspis245]

Sorry, I really try to answer all questions, but it's hard since I can't fully understand the concept.

Now I am confused. Is $F=m_2g$ correct or not?

 

[TSny]

Now I am confused. Is $F=m_2g$ correct or not?

What is meant by $F$, here? At what instant of time are you referring to?

 

[Doc Al]

Now I am confused. Is $F=m_2g$ correct or not?

In your first post, you said $F$ was the force applied to the box. If so, then no.

 

[kaspis245]

$F$ is the force with which $m_1$ is pushed downwards. It's the force that the problem asks to find. It's equivelent to $f_sp,2$.

In your first post, you said FF was the force applied to the box. If so, then no.

Please, don't tell me we start from the beginning . I just don't know what to say anymore...
Please, tell me what's wrong with this reasoning:

$m_1$ at it's highest point is affected by two downward forces: $m_1g$ and $F$ (caused by the string). At the same moment, $m_2$ will be affected by an upward spring force $F$ and downward force $m_2g$. Therefore, in order for $m_2$ to jump: $F=m_2g$.

 

[TSny]

Suggestion. Since the force of the spring can always be written as $kx$ for some value of $x$, let's agree to always use $kx$ for a spring force. (That's similar to using $mg$ for the force of gravity.) If $x$ has a certain value $x_1$, then the spring force can be written as $kx_1$. Use $F$ only for the unknown force that pushed down on $m_1$ before it was released.

Can you rewrite your argument using this notation?

 

[Doc Al]

$F$ is the force with which $m_1$ is pushed downwards.

OK, that's what I assumed.

It's the force that the problem asks to find. It's equivelent to $f_sp,2$.

Are you saying that $F$ equals the spring force?

 

[TSny]

Your notation was good in the OP:

$F+m_1g=kx$
$kx=m_2g$

But you need to be clear regarding the value of $x$ in these equations. Does the first equation refer to the initial position where $m_1$ was being held down? If so, then you could let $x_i$ be the value of $x$ for this position. Thus, replace $x$ by $x_i$ in the first equation.

If the second equation applies to the final position when $m_1$ has risen and $m_2$ is about to leave the floor, then you should use $x_f$ for $x$ in that equation.

 

[kaspis245]

Sorry, but I can't cope with your speed.

(1) When a downward force $F$ is applied to $m_1$: $kx=F+m_1g$, where $kx$ is upward spring force.

(2) When $F$ disappears, $m_1$ starts to move upwards with net force, which is equal to $kx-m_1g=(F+m_1g)-m_1g=F$. This net force can be denoted as $kx_1$.

(3) Then, when $m_1$ reaches it's highest position, the following applies: $m_1$ is affected by two downward forces: $m_1g$ and $kx_1$ (caused by the string). At the same moment, $m_2$ will be affected by an upward spring force $kx_1$ and downward force $m_2g$.

(4) Therefore, in order for $m_2$ to jump: $kx_1=m_2g$. From (2) we know, that $kx_1=F$, so the equation can be written as $F=m_2g$.

Is it clearer?

 

[Doc Al]

(2) When $F$ disappears, $m_1$ starts to move upwards with net force, which is equal to $kx-m_1=(F+m_1g)-m_1g=F$. This net force can be denoted as $kx_1$.

Only use kx to represent a spring force, not a net force on a mass. That's where you are messing up.

 

[kaspis245]

Only use kx to represent a spring force, not a net force on a mass.

How can it help? Note, that I need to find $F$.

I can do this:
From (2): $kx_1=kx-m_1g$.
In order for $m_2$ to jump: $kx_1=m_2g$, so $m_2g=kx-m_1g$.

 

[TSny]

There are two different values of $x$ that you need to work with: $x_1$ and $x_2$. See the picture below. ($x$ changes as you go from position 1 to position 2 and so the spring force changes as you go from position 1 to position 2.) In position 1, $x_1$ is related to $F$ by the fact that the net force on $m_1$ is zero in this position. In position 2, $x_2$ is related to $m_2$ by the fact that the spring is just about to lift $m_2$ off the floor.

You should be able to obtain a formula for position 1 relating $x_1$ to $F$ and a formula for position 2 relating $x_2$ and $m_2$. These formulas are essentially your equations in the OP except that you need to use the symbols $x_1$ or $x_2$ when writing the formulas.

 

[kaspis245]

These are the equations:
$F+m_1g=kx_1$
$kx_2=m_2g$

How can these equations help me?

 

[TSny]

The second equation essentially tells you the value of $x_2$. So, you can consider $x_2$ as known. The first equation let's you find the answer for $F$ if you can find the value for $x_1$.

If you can find an equation that relates $x_1$ and $x_2$, then you could solve for $x_1$. Can you think of a conservation law that applies to the system as it moves from position 1 to position 2?

 

[kaspis245]

I fail to relate $x_1$ and $x_2$. Is it correct to say that $kx_2-m_1g=m_2g$?

 

[TSny]

I fail to relate $x_1$ and $x_2$. Is it correct to say that $kx_2-m_1g=m_2g$?

No, you already had the correct relation between $x_2$ and $m_2$:

$kx_2 = m_2g$

This is the condition for the spring force to just lift $m_2$ off the floor.

 

[kaspis245]

The only relationship between $x_1$ and $x_2$ I can make is this:

When $F$ disappears, $m_1$ starts to move upwards with net force, which is equal to $kx_1−m_1g=(F+m_1g)−m_1g=F$. Only this force makes the string to expand, so obviously this force creates $kx_2$ or in other words $F=kx_2$. I really don't understand what is wrong with this reasoning. Why should I avoid $F$?

 

[TSny]

When $F$ disappears, $m_1$ starts to move upwards with net force, which is equal to $kx_1−m_1g=(F+m_1g)−m_1g=F$.

OK. This is correct.

Only this force makes the string to expand, so obviously this force creates $kx_2$ or in other words $F=kx_2$ . I really don't understand what is wrong with this reasoning

As soon as $m_1$ starts moving up, the net force will of course decrease. But you are right that the net force acting on $m_1$ at the instant just after F is removed is equal in value to F. I'm not sure what you mean when you say that "obviously this force creates $kx_2$". Anyway, it is not true that $kx_2$ has the value F. However, you might be close to the right result. Can you find an argument for showing that the net force on $m_1$ when it is at $x_1$ is the same as the net force on $m_1$ when it arrives at $x_2$? Note that the net force on $m_1$ when it arrives at $x_2$ is not $kx_2$.

Why should I avoid $F$?

Using F is fine. But it should always refer to the value of the applied force that held $m_1$ down before $m_1$ was released. In some of your earlier posts it appeared to me that you might have been using F for a spring force. But I could have been misinterpreting what you wrote.

 

[kaspis245]

Well, I think the upward net force acting on $m_1$ in position $x_1$ is the same force which creates a downward net force in position $x_2$, so maybe this applies:
$kx_1-m_1g+F=kx_2+m_1g$

Then I used these equations:

$F+m_1g=kx_1$
$kx_2=m_2g$

And got $F=\frac{g(m_1+m_2)}{2}$.

Does this happen to be the correct answer?

 

[TSny]

Well, I think the upward net force acting on $m_1$ in position $x_1$ is the same force which creates a downward net force in position $x_2$, so maybe this applies:
$kx_1-m_1g+F=kx_2+m_1g$

The left side should represent the upward net force at $x_1$ after the applied force F is removed.

 

[kaspis245]

Sorry, $kx_1-m_1g-F=kx_2+m_1g$. Now I see that it gets me nowhere...

 

[TSny]

You still don't have the left side correct. There are only two forces that act on $m_1$ after F is removed.

 

[kaspis245]

Sorry again: $kx_1-m_1g=kx_2+m_1g$.