Kaustubh sri
- 22
- 0
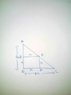
Find the length of largest square accommodated in a right angled triangle whose perpendicular length is 16 m and base's length is 8 m.
My attempt
I have tried a lot to find the length but every time it comes in fraction , i think that the figure i have made is wrong
. The answer I am getting is 16/3,could anybody tell me whether i am right or wrong.
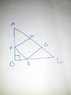
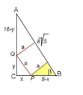
My attempt
I have tried a lot to find the length but every time it comes in fraction , i think that the figure i have made is wrong
. The answer I am getting is 16/3,could anybody tell me whether i am right or wrong.