- #1
Buzz Bloom
Gold Member
- 2,519
- 467
- Homework Statement
- Note: I use the notation []’ to indicate d[]/dt. This is because I do not have a convenient way to use the dot notation for differentiation.
In equation [3] below, what are the constrains on the Ωs (in addition to those given in the Relevant equations [8], [9], and [10]) such that there is a value, t=s satisfying [1] and [2]?
- Relevant Equations
- See below in Solution section.
Required Equations
Note: Includes inequalities.
[1] H(s) = 0, and
[2] H’(s) = 0?
[3]
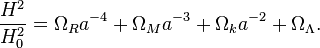
[4] H = a’/a
[5] a(t0) = a0 =1
[6] H0 = H(t0)
[7] ΩR = 0
[8] Ωk<0, Ωk = -K, K > 0
[9] ΩM>1, ΩM = M, M > 1
[10] ΩΛ = 1-Ωk- ΩM = 1+K-M > 0 → M-1 < K
Solution
Note: I have assigned this problem to myself. I would appreciate a response that confirms that my solution is correct, or identifies one or more steps where I made a mistake.
The inequality in [29] is the solution as a final constraint on of the Ωs (in addition to
he inequalities in [8] through [10]). Below are the sequence of steps leading to [29].
Note that [1] and [4] implies that a’(s) = 0.
Using [4] through [10], [3] becomes
[11a] a’2/a2 = H02 [ M/a3 – K/a2 + (1-M+K)].
In [1] and [2], s is defined as the value of t that satisfies [1] and [2].
Note that [1] and [4] implies that
[11b] a’(s) = 0.
Let
[11c] b=a(s).
Using [11b] and [11c] simplifies [11a] to
[12] 0 = M/b3 – K/b2 + (1-M+K).
Multiplying [12] by b3 yields
[13] 0 = M – Kb + (1-M+K)b3
Equation [13] defines the specific value a=b which satisfies condition [1].
I now proceed to work with [2].
Differentiating [4] with respect to t yields
[14] H’ = a’’/a – a’2/a2 = (a’’/a - H2)
Using [1] in [14] yields
[15] a’’(s) = 0.
Multiplying [11a] by a3 yields
[16] a a’2 = H02 [M - Ka +(1-M+K)a3]
Differentiating [16] with respect to t yields
[17] a’3+2aa’a’’ = H02 [-Ka’ +3(1-M+K)a2a’]
Dividing [17] by a’ yields
[18a] a’2+2aa’’ = H02 [-K +3(1-M+K)a2]
Using [1], [11c], and [15] in [18a] yields
[18b] 0 = -K +3(1-M+K)b2
Solving [18b] for b2 yields
[19] b2 = K/(3(1-M+K)).
Inequality [10] implies that b2 is positive, so b is a real number.
Substituting [19] into [13] yields
[20] 0 = M – Kb + (K/(3(1-M+K))) (1-M+K)b]
Simplifying [20] yields
[21] M = Kb(1-(1/3)) = (2/3)Kb, which yields
[22] b = (3/2)M/K.
I will now check to confirm that [22] and [19] together are a solution of [13].
[23] b2 = (9/4) M2/K2 = K/(3(1-M+K)) yields
[24a] M2(1-M+K) = (4/27)K3, which yields
[24b] 1-M+K = (4/27)K3/M2.
Combining [24b] with [13] yields
[25a] 0 = M – Kb + ((4/27)K3/M2) b3
Combining [19] and [22] yields
[23] (9/4) M2/K2 = K/(2(1-M+K)), yields
[24] K= (9/2)M2(1-M+K), yields
[25] K(1+(9/2)M2) = (9/2)M2, yields
[26] K = (9/2)M2 / (1+(9/2)M2) = M2/((2/9)+M2), yields
[27a] 1/K = 1 + (2/9)/M2,yields
[27b] 1/M2 = (9/2) [(1/K)-1] = (9/2)((1-K)/K), and
[28] M2 = (2/9) K/(1-K).
Equation [28] implies that
[29] K<1,
since otherwise M would not be a real number.
Combining [29] with [9] and [10] yields a summary inequality:
[30] 0 < M-1 < K < 1.
NOTE:
I have also made an effort to also show that
Note: Includes inequalities.
[1] H(s) = 0, and
[2] H’(s) = 0?
[3]
[4] H = a’/a
[5] a(t0) = a0 =1
[6] H0 = H(t0)
[7] ΩR = 0
[8] Ωk<0, Ωk = -K, K > 0
[9] ΩM>1, ΩM = M, M > 1
[10] ΩΛ = 1-Ωk- ΩM = 1+K-M > 0 → M-1 < K
Solution
Note: I have assigned this problem to myself. I would appreciate a response that confirms that my solution is correct, or identifies one or more steps where I made a mistake.
The inequality in [29] is the solution as a final constraint on of the Ωs (in addition to
he inequalities in [8] through [10]). Below are the sequence of steps leading to [29].
Note that [1] and [4] implies that a’(s) = 0.
Using [4] through [10], [3] becomes
[11a] a’2/a2 = H02 [ M/a3 – K/a2 + (1-M+K)].
In [1] and [2], s is defined as the value of t that satisfies [1] and [2].
Note that [1] and [4] implies that
[11b] a’(s) = 0.
Let
[11c] b=a(s).
Using [11b] and [11c] simplifies [11a] to
[12] 0 = M/b3 – K/b2 + (1-M+K).
Multiplying [12] by b3 yields
[13] 0 = M – Kb + (1-M+K)b3
Equation [13] defines the specific value a=b which satisfies condition [1].
I now proceed to work with [2].
Differentiating [4] with respect to t yields
[14] H’ = a’’/a – a’2/a2 = (a’’/a - H2)
Using [1] in [14] yields
[15] a’’(s) = 0.
Multiplying [11a] by a3 yields
[16] a a’2 = H02 [M - Ka +(1-M+K)a3]
Differentiating [16] with respect to t yields
[17] a’3+2aa’a’’ = H02 [-Ka’ +3(1-M+K)a2a’]
Dividing [17] by a’ yields
[18a] a’2+2aa’’ = H02 [-K +3(1-M+K)a2]
Using [1], [11c], and [15] in [18a] yields
[18b] 0 = -K +3(1-M+K)b2
Solving [18b] for b2 yields
[19] b2 = K/(3(1-M+K)).
Inequality [10] implies that b2 is positive, so b is a real number.
Substituting [19] into [13] yields
[20] 0 = M – Kb + (K/(3(1-M+K))) (1-M+K)b]
Simplifying [20] yields
[21] M = Kb(1-(1/3)) = (2/3)Kb, which yields
[22] b = (3/2)M/K.
I will now check to confirm that [22] and [19] together are a solution of [13].
[23] b2 = (9/4) M2/K2 = K/(3(1-M+K)) yields
[24a] M2(1-M+K) = (4/27)K3, which yields
[24b] 1-M+K = (4/27)K3/M2.
Combining [24b] with [13] yields
[25a] 0 = M – Kb + ((4/27)K3/M2) b3
= M – K (3/2)M/K + ((4/27)K3/M2) (27/8)M3/K3
= M – (3/2)M + (1/2)M
= 0.
Combining [19] and [22] yields
[23] (9/4) M2/K2 = K/(2(1-M+K)), yields
[24] K= (9/2)M2(1-M+K), yields
[25] K(1+(9/2)M2) = (9/2)M2, yields
[26] K = (9/2)M2 / (1+(9/2)M2) = M2/((2/9)+M2), yields
[27a] 1/K = 1 + (2/9)/M2,yields
[27b] 1/M2 = (9/2) [(1/K)-1] = (9/2)((1-K)/K), and
[28] M2 = (2/9) K/(1-K).
Equation [28] implies that
[29] K<1,
since otherwise M would not be a real number.
Combining [29] with [9] and [10] yields a summary inequality:
[30] 0 < M-1 < K < 1.
NOTE:
I have also made an effort to also show that
b > a0 = 1.
My intuition tells me that this must be true, but I have failed to prove it. I have decided to discuss the implications of a possibleb < a0 = 1
in a separate thread.
Last edited: