Find the moment of inertia of the system

Join the discussion
Registration is free. Start your own thread to ask a follow-up.
Sign up Log in
1 reply · 2K views
awillso
Messages
1
Reaction score
0
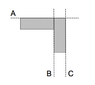
Two rectangular objects, each 1.0 m by 3.0 m, are attached as shown. Each rectangle has a mass of 1.5 kg. Find the moment of inertia of the system about (a) axis A, (b) axis B, and (c) axis C.

I have no idea what to do, any help is appreciated.
 
Attachments
  • Screen Shot 2015-03-09 at 8.24.25 PM.png
    Screen Shot 2015-03-09 at 8.24.25 PM.png
    1.5 KB · Views: 561
Physics news on Phys.org

Discussion

According to the forum rules, you need to make an effort to solve the problem before we can help. What do you know about moment of inertia? Do you know how to calculate it in simple cases?
 

Similar threads

High School How to find the Moment of Inertia for a Sphero robot?
  • GopherTv
  • · Replies 4 ·
  • Mechanics
Replies
4
Undergrad How to find moment of inertia of an insect?
  • potatoboy
  • · Replies 5 ·
  • Mechanics
Replies
5
High School Moment of Inertia of Rectangles
  • al4n
  • · Replies 3 ·
  • Mechanics
Replies
3
Undergrad Moment of inertia of human body with limbs at an angle
  • sunsetpearl
  • · Replies 12 ·
  • Mechanics
Replies
12
Undergrad Moment of inertia and contact force
  • GT1
  • · Replies 7 ·
  • Mechanics
Replies
7
Undergrad Resolve moment of inertia at an angle
  • curiousPep
  • · Replies 2 ·
  • Mechanics
Replies
2
Undergrad How find moment of inertia for car in turn?
  • user079622
  • · Replies 49 ·
  • Mechanics
2
Replies
49
Undergrad Moment of Inertia about an axis and Torque about a point
  • Nikhil_RG
  • · Replies 5 ·
  • Mechanics
Replies
5
Undergrad Importance of Moment of Inertia for designing helicopters and propellers?
  • OnlyPhysics
  • · Replies 2 ·
  • Mechanics
Replies
2
High School Why does torque increase with increasing moment of inertia?
  • makamo66
  • · Replies 13 ·
  • Mechanics
Replies
13