Find the particle's charge in terms of Q.

[Gnall]

Homework Statement

I have found the first following, I need b and c. The question is:

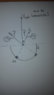
A total positive charge Q is uniformly distributed on an insulating thread of length L. The thread is bent into the shape of a semicircle and located in the xy plane, as shown in the figure. Express your answers in terms of the given quantities and fundemental constants as needed.
I found a following.
b.) If a charged particle with a mass m is located at the point x=0, y=L; the electric potential at P becomes zero. Find the particle's charge in terms of Q.
c.) If the charged particle at (b) is first carried to a point P, and then given an initial velocity v0 in the positive y direction, find the minimum value of v0 such that the particle escapes to a point infinitely far away from the charged thread. Ignore any gravitational effects.

Relevant Equations

Electric potential of semicircle at P point in the first following :
V= kQ/R

For the b following:
kQ/R=kq/L
L=πR
kQ/R=kq/πR
πQ=q

 

[haruspex]

kQ/R=kq/L

How does that make the net potential zero?

 

[Gnall]

How does that make the net potential zero?

Because, the electric potential due to the semicircle at P point is (kQ/R) and, due to the q charge is (kq/L). So I equalized them. Is that wrong for electric potential?

 

[gneill]

Because, the electric potential due to the semicircle at P point is (kQ/R) and, due to the q charge is (kq/L). So I equalized them. Is that wrong for electric potential?

How do the two potentials sum at point P?

 

[Gnall]

How do the two potentials sum at point P?

The direction of electric potential due to the semicircle is in +y direction. Because the Vx components will cancel due to the symmetry. Like in the image.

 

[gneill]

The direction of electric potential due to the semicircle is in +y direction. Because the Vx components will cancel due to the symmetry. Like in the image.

Potential has no direction. I'ts a scalar value.

 

[PeroK]

The direction of electric potential due to the semicircle is in +y direction. Because the Vx components will cancel due to the symmetry. Like in the image.

You're the second person today to think that potential has a direction. It has a sign, based on the sign of the charge, but it's not a vector. It doesn't have $V_x$ and $V_y$ components.

 

[Gnall]

How do the two potentials sum at point P?

And to make the potential zero at the point P, there should be electric potential at opposite
(-y)direction due to the charged particle at (x,y)=(0,L)

You're the second person today to think that potential has a direction. It has a sign, based on the sign of the charge, but it's not a vector. It doesn't have VxVx and VyVy components.

So how to make electric potential zero at P?

 

[Gnall]

Potential has no direction. I'ts a scalar value.

So how to make electric potential zero at P?

 

[PeroK]

So how to make electric potential zero at P?

You could use a charge of the opposite sign.

 

[Gnall]

You could use a charge of the opposite sign.

Oh okay. So the equation is the same except the sign of the second charge?

 

[PeroK]

Because, the electric potential due to the semicircle at P point is (kQ/R) and, due to the q charge is (kq/L). So I equalized them. Is that wrong for electric potential?

Potentials add. So, you need $V_1 + V_2 = 0$.

 

[Gnall]

Potentials add. So, you need $V_1 + V_2 = 0$.

Understood. So what about the third question? How can I solve?

 

[PeroK]

Understood. So what about the third question? How can I solve?

Have you any ideas? Potentials, fields, forces, energies?

 

[Gnall]

Have you any ideas? Potentials, fields, forces, energies?

Yes actually. I thought E=qV
Then V is kQ/R
Kinetic energy is 1/2mVsquare
So maybe I can equalize V and kinetic energy?

 

[PeroK]

Yes actually. I thought E=qV
Then V is kQ/R
Kinetic energy is 1/2mVsquare
So maybe I can equalize V and kinetic energy?

I guess that means conservation or energy, potential and kinetic?

 

[Gnall]

I guess that means conservation or energy, potential and kinetic?

Yes but I don't have any idea except that. Should I use F=q.E?

 

[Gnall]

I guess that means conservation or energy, potential and kinetic?

Besides, question says ignore the gravitational force.

 

[PeroK]

Yes but I don't have any idea except that. Should I use F=q.E?

It's not necessary to calculate the forces: that is one advantage of using potential. There's a page here about electrostatic potential energy:

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elepe.html

 

[Gnall]

I guess that means conservation or energy, potential and kinetic?

Question says

It's not necessary to calculate the forces: that is one advantage of using potential. There's a page here about electrostatic potential energy:

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elepe.html

Sorry actually I wanted to mean E=qV=kqQ/R instead of V. So I should equalize qV to 1/2mVsquare?

 

[Gnall]

It's not necessary to calculate the forces: that is one advantage of using potential. There's a page here about electrostatic potential energy:

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elepe.html

So,
Ep1 + Ek1 = Ep2 + Ek2 so,
kQq/R + 0 = 0 + 1/2mVsquare
Is that true?

 

[PeroK]

So,
Ep1 + Ek1 = Ep2 + Ek2 so,
kQq/R + 0 = 0 + 1/2mVsquare
Is that true?

You need to be more careful about signs and what these quantities mean. I would say that at infinity both PE and KE are 0. If the charge just has enough energy to make it.

 

[Gnall]

You need to be more careful about signs and what these quantities mean. I would say that at infinity both PE and KE are 0. If the charge just has enough energy to make it.

Oh, yes you are totaly right.
kQq/R + 1/2mvsquare = 0+0?
Is that true? :)

 

[Gnall]

Oh, yes you are totaly right.
kQq/R + 1/2mvsquare = 0+0?
Is that true? :)

You need to be more careful about signs and what these quantities mean. I would say that at infinity both PE and KE are 0. If the charge just has enough energy to make it.

Oh finally! :) Thank you so much sir, I'm very apreciated.