Find the set of possible values of ##a## - Modulus Graph

[chwala]

Homework Statement

See attached

Relevant Equations

Modulus equations

My interest is on question 9. b(i)

Find the question and solution here;

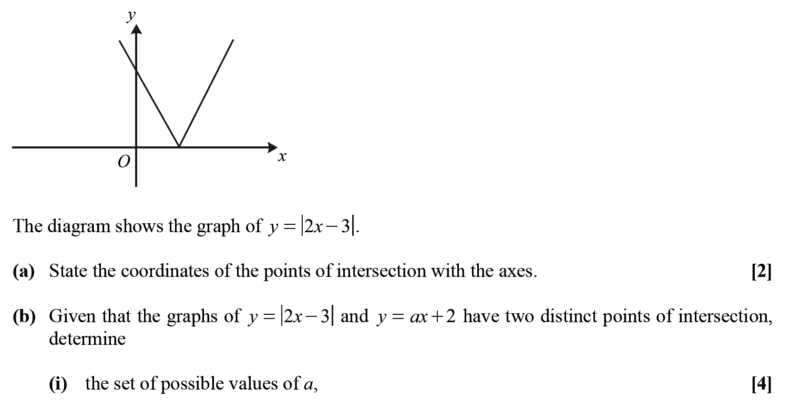
I understand that $a$ should be less than $2$ because when $a=2$, the two equations shall have same gradients which implies that the two lines are parrallel to each other. Now to my question, this solution does not look entirely correct because we have other values of $a$ less than $2$ that will not satisfy the equations...for. e.g if $a=-2$...
The correct solution would be $-1.33≤a< 0$ or $0<a<2$

 

[anuttarasammyak]

-4/3 < a < 2 which does not include a= -4/3

 

[chwala]

-4/3 < a < 2 which does not include a= -4/3

@anuttarasammyak...but $a≠0$ the inequality
$-\frac {4}{3}$$<a<2$ is not continous...your inequality may not be correct.

Probably to determine the other value of $a=-\frac {4}{3}$ one would use

$y=ax+2$
$0=1.5a+2$
$0=3a+4$
$-3a=4$
$a$=$-\frac {4}{3}$

 

[SammyS]

@anuttarasammyak...but $a≠0$ the inequality
$-\frac {4}{3}$$<a<2$ is not continous...your inequality may not be correct.

Probably to determine the other value of $a=-\frac {4}{3}$ one would use

$y=ax+2$
$0=1.5a+2$
$0=3a+4$
$-3a=4$
$a$=$-\frac {4}{3}$

Why do you say $a\ne 0 ~ ?$

To find a lower bound to $a$, consider what the $x$-intercept is for $y=|2x-3|$.

 

[chwala]

Why do you say $a\ne 0 ~ ?$

To find a lower bound to $a$, consider what the $x$-intercept is for $y=|2x-3|$.

Arrrghh ...true. Cheers man! $a=0$ is correct too.

 

[SammyS]

Probably to determine the other value of $a=-\frac {4}{3}$ one would use

$y=ax+2$
$0=1.5a+2$
$0=3a+4$
$-3a=4$
$a$=$-\frac {4}{3}$

So, are you saying that $a=-\dfrac {4}{3}$ is a valid solution for $a ~ ?$

If so, what are the two distinct points of intersection ?

 

[chwala]

So, are you saying that $a=-\dfrac {4}{3}$ is a valid solution for $a ~ ?$

If so, what are the two distinct points of intersection ?

No, what I indicated is rather the approach that a student may use in determining the required values of $a$...I hope that's clear.
The correct solution is as indicated in post $2$.

 

[chwala]

My apologies on this...,

The markscheme was correct! i ought to have checked all the pages!... Kindly find the full solution here.
Thanks @anuttarasammyak and @SammyS on your contribution.