Find the Speed of Blocks A & B After Moving 2.70cm

  • Thread starter Thread starter TinaChan90
  • Start date Start date
  • Tags Tags
    Blocks Speed
AI Thread Summary
To find the speed of blocks A and B after moving 2.70 cm, one can apply Newton's laws and consider the forces acting on both blocks, including gravitational force and friction. The kinetic friction between block A and the tabletop plays a crucial role in determining the net force and acceleration of the system. Using energy methods or kinematic equations can also help in solving for the final velocity after the specified distance. The discussion highlights the importance of understanding velocity beyond circular motion, as it is a fundamental concept in various physics problems. A clear setup of the problem is essential for accurate calculations.
TinaChan90
Messages
1
Reaction score
0
As shown in the figure , block A (mass 2.20kg ) rests on a tabletop. It is connected by a horizontal cord passing over a light, frictionless pulley to a hanging block B (mass 2.27kg ). The coefficient of kinetic friction between block A and the tabletop is 0.344.

problem.jpg


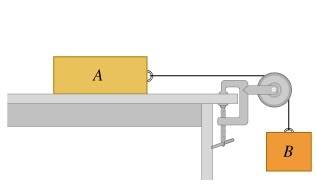
After the blocks are released from rest, find the speed of each block after moving 2.70cm
---

Asking for V.

And I am so confused since we only only use V in circular motion, So I don't even know how to set it up
 
Physics news on Phys.org
Are you familiar with energy methods, Newton's laws, and / or the kinematic equations?? The velocity or speed is used quite often in Physics problems, so surely you must have seen it other than in circ motion problems, is that right??
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Newton's law problem: Pushing 2 stacked blocks on a horizontal table
Replies
13
Views
3K
Why can we move the spring with constant speed when we apply a force?
Replies
29
Views
2K
Body attached to a block by a spring, shaped like an inclined plane
Replies
1
Views
901
Virtual displacement for a block sliding down a wedge
Replies
3
Views
2K
Can a 10N Force Overcome Friction to Move a 10kg Block?
Replies
2
Views
1K
Find acceleration of Moving incline with a block on it
Replies
11
Views
3K
Dynamics of a Block on top of a slab with friction between them
Replies
33
Views
1K
Deriving motion equations for two blocks on a rough table
Replies
11
Views
2K
Forces/Dynamics: A block sliding on a plate
Replies
45
Views
7K
Time period of SHM & Energy conservation in pulley-spring-block system
Replies
24
Views
3K

Hot Threads

Recent Insights

Back
Top