ryty
- 30
- 0
Homework Statement
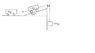
Two 1kg carts and a 500g weight are linked with cables. One of the carts sits on a 15°
ramp, while the other is on a horizontal surface. See diagram. Find the tension in the
cable linking the two carts.
i attached the picture.
Homework Equations
im not sure, but i think its T-mg=ma
but since there are two carts on top, and one is on a ramp, i don't think this is right
The Attempt at a Solution
F(weight 3)=.5 kg*9.8 m/s^2= 4.9 N
F(weight 2)=1 kg*9.8m/s^2*sin(15)=2.54 N
F(weight 1)=1kg*9.8m/s^2=9.8 N
im not sure what to do next