SUMMARY
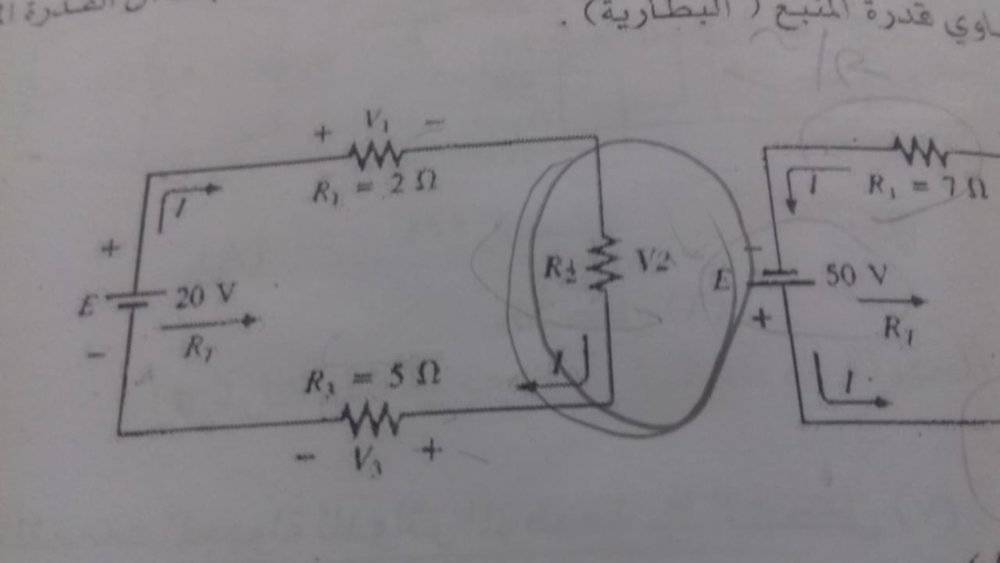
The discussion focuses on finding the unknown resistance R2 in a series circuit with given values R1 = 2Ω, R3 = 5Ω, and E = 20V. Participants emphasize the application of Kirchhoff's Voltage Law (KVL) to relate the voltages across the resistors and the total voltage. The consensus is that without knowing the current (I) or the resistance R2, it is impossible to derive a unique solution. Instead, users are encouraged to explore various hypothetical values for R2 to understand the relationship between the circuit parameters.
PREREQUISITES
- Understanding of Kirchhoff's Voltage Law (KVL)
- Basic knowledge of series circuits
- Familiarity with Ohm's Law
- Ability to manipulate algebraic equations
NEXT STEPS
- Explore the application of Kirchhoff's Voltage Law in complex circuits
- Learn how to calculate current and voltage in series circuits
- Investigate symbolic solutions for unknown variables in electrical circuits
- Study the impact of varying resistance values on circuit behavior
USEFUL FOR
Electrical engineering students, hobbyists working with circuits, and anyone interested in understanding series circuit analysis and problem-solving techniques.