spj1
- 7
- 0
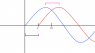
I have a question asking for the period, frequency, amplitude and phase angle from simply looking at a graph. I have the period and frequency, and 'think' i have the amplitude (high point - low point / 2), but I don't know how to get the phase angle. No equation is given so I can't simply consider the coefficients in front of sin and cos.
Can anyone point me in the right direction?
Can anyone point me in the right direction?