your answer is correct !,will you try to use geometry ?anemone said:My solution:
This is most likely not what you're looking for but I couldn't resist to solve any given geometry problem with the help of my close friend, aka trigonometry, hehehe...:p
View attachment 3568
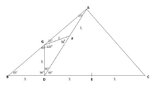
First let $BD=DE=EC=k$ and join DG and GF such that $\angle ABC=45^{\circ}=\angle DGB$, $\angle GDF=30^{\circ}=\angle DFG$ and $\angle DAB=15^{\circ}=\angle AGF$ so triangles $DBG$, $DGF$ and $AGF$ are isosceles with the congruent sides labeled as $k$.
Applying the Sine Rule to the triangle $DFG$ we have
$\dfrac{DF}{\sin 120^{\circ}}=\dfrac{k}{\sin 30^{\circ}}\,\,\,\implies DF=\sqrt{3}k$
Applying the Cosine Rule to the triangle $ACD$ we get
$AC^2=(2k)^2+((1+\sqrt{3})k)^2-2(2k)(1+\sqrt{3})k)\cos 60^{\circ}\,\,\,\implies AC=\sqrt{6}k$
Applying the Sine Rule again to the triangle $ACD$ we see that
$\dfrac{AC}{\sin 60^{\circ}}=\dfrac{AD}{\sin ACB}$
$\sin ACB=\dfrac{1+\sqrt{3}}{2\sqrt{2}}=\dfrac{1}{2}\cdot\dfrac{1}{\sqrt{2}}+\dfrac{\sqrt{3}}{2}\cdot\dfrac{1}{\sqrt{2}}=\sin 30^{\circ}\cos 45^{\circ}+\cos 30^{\circ}\sin 45^{\circ}=\sin(30^{\circ}+45^{\circ})=\sin 75^{\circ}$
$\therefore \angle ACB=75^{\circ}$.
Albert said:
To find the measure of $\angle ACB$ in $\triangle ABC$, use the Law of Cosines or the Law of Sines. The Law of Cosines states that $c^2 = a^2 + b^2 - 2ab\cos\angle C$, where $a$ and $b$ are the lengths of the sides adjacent to $\angle C$ and $c$ is the length of the side opposite to $\angle C$. The Law of Sines states that $\frac{a}{\sin\angle A} = \frac{b}{\sin\angle B} = \frac{c}{\sin\angle C}$.
To find the measure of $\angle ACB$ in $\triangle ABC$, you need to know the lengths of at least two sides and the measure of the angle opposite to one of those sides. This can be done using the Law of Cosines or the Law of Sines.
No, the Pythagorean Theorem can only be used to find the lengths of sides in a right triangle. It cannot be used to find the measures of angles.
Yes, you can also use the properties of similar triangles or the Angle Bisector Theorem to find $\angle ACB$ in $\triangle ABC$. These methods involve setting up proportions and solving for the unknown angle.
In an equilateral triangle, all angles are congruent, meaning they have the same measure. Therefore, in an equilateral triangle $\angle ACB$ would have a measure of $60^{\circ}$ or $\frac{\pi}{3}$ radians.
