Finding best fit distribution and its Parameters

AI Thread Summary
The discussion focuses on finding the best fit distribution and its parameters for a dataset after normalizing histograms. The user has attempted a logarithmic fit but found it unsuitable due to negative values. Suggestions include using a Poisson distribution and exploring Log-Normal distribution as an alternative. To implement this in Excel, it’s recommended to define Y as Log(X) and plot the frequencies of X against Y, potentially using Excel's logarithmic axis option. The goal is to identify the most appropriate distribution for the data.
shegal
Messages
3
Reaction score
0
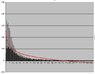
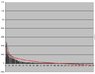
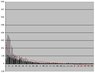
Thanks to EnumaElish for helping me in Normalizing the histograms. I now want to find the best fit distribution and what will be the parameters for that distribution. I tried lograthmic but it goes in negative and also is not much fit (the new plots are attached). If I use poisson what will be the parameters. Please help me in finding the bestfit distribution and its parameters.
 

Attachments

  • LL_DDoS_V1_Inside_Normalized.JPG
    LL_DDoS_V1_Inside_Normalized.JPG
    17.1 KB · Views: 578
  • LL_DDoS_v1_Outside_Normalized.JPG
    LL_DDoS_v1_Outside_Normalized.JPG
    16.7 KB · Views: 679
  • LL_DDoS_V2_Inside_Normalized.JPG
    LL_DDoS_V2_Inside_Normalized.JPG
    18.4 KB · Views: 545
Physics news on Phys.org
I'd try Log-Normal, per my previous advice.
 
How would you do this in excel.
 
Define Y = Log(X) where X is your original variable on the X-axis (apparently goes from 1 to 365 or so). Then plot the associated frequencies (of X) against Y. Excel might have a plotting option that let's you express either axis in Log form; if so, you can select that option to logarithmize the X axis.
 
Last edited:

Similar threads

I Parameters of a distribution of a physical variable
Replies
4
Views
2K
A LogLikelihood - Poisson distribution
Replies
2
Views
2K
A Correlation between parameters in a likelihood fit
Replies
3
Views
1K
I Akaike Information Criterion Vs Likelihood Ratio Test
Replies
5
Views
4K
I Conf.intervals for fitted parameters: divide by sqrt(n)?
Replies
7
Views
2K
I Plot Linear Fit w/ Error Bounds: y=ax+b
Replies
3
Views
2K
I What Does the Likelihood Function Tell Us?
Replies
16
Views
2K
I Extract error from simulated data
Replies
13
Views
2K
I Understanding Confidence Intervals for Fit Parameters
Replies
3
Views
2K
A How to perform a fit with correlated variables
Replies
16
Views
3K

Hot Threads

Recent Insights

Back
Top