Finding charge and mass on hanging strings

[nilesthebrave]

Homework Statement

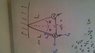
Two identical point charges with a mass <i>m</i> and equal charge <i>q</i> repel each other at the end of a lightweight rope of length L=12.5cm. The angle θ is 17.5 degrees.
a)What is the mass <i>m</i>?
b)What is the charge <i>q</i>?

Homework Equations

Fx= Fe-Tcosθ=0
Fy=mg-Tsinθ=0

Fe=kq1q2/r^2

The Attempt at a Solution

I have a free body diagram drawn up(don't know how to post them sorry) of the left ball, with the Fg acting downwards, the Ft acting towards the connecting point with the ceiling and the Fe pointing horizontally away from the opposite sphere.

The problem I'm having is I don't know how to find the mass since it seems no matter how I try to go about solving this equation I always have two unknowns.

I cannot tell if I'm just missing something simple by looking too hard at it, but I can't seem to figure out where to start. Any suggestions?

 

[TSny]

I agree with you. Too many unknowns. You could set the mass at any value you want and then find the charge that would make them hang at the given angle, or vice versa.

 

[nilesthebrave]

I've e-mailed my professor now, since I'm still completely lost on this.

 

[TSny]

Good, let us know what he/she says.

 

[nilesthebrave]

Alright, after working some other problems I tried to come back to this one from a different angle. Let's see if this works:

m1gsinθ1=Fsinθ1

m2gsinθ2=Fsinθ3

m1gsinθ1=m2gsinθ2

sinθ2=msinθ1

sin17.5 degrees=msin17.5 degrees

0.300=0.300m

1kg=m

b) q=2Lsinθ √((mg/k)tanθ)

q=2(.125)sin17.5√((1(9.8)/(9x10^9))tan17.5)

q=0.0752(1.85x10^-5)

q=1.39 x 10^-6 Coulombs


I don't know if that's right, but it gave me an answer and it'll at least count for partial credit I think if it's not. But if anyone has any comments/corrections I'd love to hear them, since I would rather understand this stuff

 

[TSny]

Hmm. You set m = 1 kg (which is a very large mass for this type of problem!). I thought m was something you were suppose to determine?

However, your expression for q in part (b) looks good. Did you derive this expression?

 

[nilesthebrave]

I got m, from the first set of equations I used. Which got me to

sinθ1=m sinθ2

I thought 1kg was pretty high as well, but seeing as this is due in half an hour and my professor never responded I did what I had to do.

As for part b of the question I took:

Ftsinθ=Fe=(kq^2)/(2Lsinθ)^2
Ftcosθ=Fg=mg

I then divided these two expressions to get

tanθ=(kq^2)/mg(2Lsinθ)^2

q=2Lsinθ√((mg/k)tanθ)

then just plugged everything in(including my 1kg mass that I found in part a)

Crossing my fingers that I did this right

 

[TSny]

Alright, after working some other problems I tried to come back to this one from a different angle. Let's see if this works:

m1gsinθ1=Fsinθ1

m2gsinθ2=Fsinθ3

m1gsinθ1=m2gsinθ2

sinθ2=msinθ1

m1 = m2, so the masses and g cancel out in the next to last equation. So you just get sinθ1=sinθ2. Can't get the mass this way.
[I don't see where these equations come from.]

 

[TSny]

I think you're better off just stating that the problem can't be solved as stated.

Anyway, good luck!

 

[Dickfore]

Hint:
<br /> r = 2 L \, \sin \theta<br />

 

[Darth Frodo]

I'm a little puzzled...

m1gsinθ1=Fsinθ1

Therefore given that m is one F should be 9.8N

When using q = q=1.39 x 10^-6 C I'm afraid I get 4810N.


Can you please post a free body diagram. Simply select "Manage Attachments"

 

[Dickfore]

Therefore given that m is one F should be 9.8N

Where did you see this as given?

 

[Darth Frodo]

Well if mgsinθ1 = Fsinθ1

m = 1

gsinθ1 = Fsinθ1

F = g

This was just a test I did to show if m was equal to 1 then q should equal what the OP got but I don't think it does.

 

[Dickfore]

The charge and the mass cannot be found independently. All you can do is find the ratio q^2/m.

 

[Darth Frodo]

Alright, after working some other problems I tried to come back to this one from a different angle. Let's see if this works:

m1gsinθ1=Fsinθ1

m2gsinθ2=Fsinθ3

m1gsinθ1=m2gsinθ2

sinθ2=msinθ1

sin17.5 degrees=msin17.5 degrees

0.300=0.300m

1kg=m

b) q=2Lsinθ √((mg/k)tanθ)

q=2(.125)sin17.5√((1(9.8)/(9x10^9))tan17.5)

q=0.0752(1.85x10^-5)

q=1.39 x 10^-6 Coulombs

All I did was use first equation to check if the answer of m = 1 was true with the value of q achieved but it wasn't. Therefore the answer can't be right?

 

[TSny]

I'm a little puzzled...

m1gsinθ1=Fsinθ1

Darth, This equation given by the OP is not correct. It's not clear which force F stands for here. But whether F stands for the electric force or the tension in the string, it is still not correct.

In the original post, the OP essentially stated the correct relevant equations if θ is measured from the horizontal. However, I suspect that the angle that was given in the problem is measured from the vertical. If so, sinθ and cosθ should be switched in the equations.

 

[Darth Frodo]

Yeah, thanks TSny, I jut wasn't sure and it's really hard to tell without the OP's diagram

 

[Yukoel]

Hello nilesthebrave,
I assume your question says " there are two branches of the rope each containing the unknown charge with unknown mass at their ends ".From the free body diagram I get from this interpretation there are three concurrent forces on each charge namely the tension of the string(T),The weight (W) and electrostatic force of repulsion(F).The angles between them are clearly obtainable (using the inclination of one string as given).If you use lami's theorem for equilibrium in case of concurrent forces it is evident that you can at best obtain the ratio of the square of the charge to the mass.This is based on my interpretation though.You need to post a picture of your case.

regards
Yukoel

 

[nilesthebrave]

Thank you very much for all the replies.

I got to class and nobody had even touched this problem, so I may have done it wrong but I at least have some chicken scratches for partial credit.

I've included a diagram of what the problem looks like. It's too late for me to fix my answer but I still want to know how to solve such a problem for the sake of knowledge.

Also, does anybody know of a good Physics 2 textbook? I've ordered the one Berkeley uses since I've heard a few recommendations. Our school uses the W.H. Freeman and Company textbooks for the first three semesters of Physics, and what I have experienced so far with the first book and the first few chapters of the second book makes me longing for something that doesn't drip in suck.

Thanks again everyone!

 

[nilesthebrave]

Sorry for double post, but I forgot to upload the picture of the diagram.

 

[nilesthebrave]

Sorry again, just not my day for technology. Here's a picture that's oriented properly.