Finding current and Power delivered to Resistors

[elizabethrae]

Homework Statement

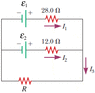
In the figure below, find the following. (Let E1 = 26.0 V, E2 = 13.0 V, and R = 9.0 Ω.)
(attachment)

(a) the current in each resistor
I1 =
I2 =
I3 =

(b) the power delivered to each resistor
P1 =
P2 =
P3 =

Homework Equations

V=IR, Req=R1+R2 for resistors in series, Req=1/R1 + 1/R2 for resistors in parallel

The Attempt at a Solution

Ok so I figured for at least I1 I could use the V=IR equation but I keep getting the wrong answer. Would I have to find the total resistance of all the resistors and then use Req in the equation with E1 for I1? Thanks

 

[gneill]

That lone resistor R is what prevents you from just applying V=IR. The current I3 = I1 + I2 passes through it on the way back to the battery negative terminal.

One way or another you'll have to solve for the currents or at least the voltage at the "top" of R (so you can compute voltage differences across all the resistors).

There are several possible approaches, depending upon how far along in your studies you are. Pick a method you're familiar with. Maybe Kirchoff node or loop methods, or Thevenin-Norton transformations.

 

[elizabethrae]

I'm still kinda lost as to how to start it.. we've learned the node and volatge laws and I think we are supposed to use them but I am not sure how. I don't have any values for current so I can't really use the node law, and what significance is V1+V2-V=0? I'm still just confused :S

 

[gneill]

Well, try the node voltage method. Take the place where the resistors all connect as one node. Call it node A. Set the "common" node as the place where the two batteries meet (it may be helpful to picture the circuit diagram rotated 90 degrees to the left so that node A is on top).

Now suppose the voltage at node A is VA. Can you write the equations for the branches that connect to that node?

 

[Bashyboy]

I am actually working on precisely the same problem, with the exception that \mathcal{E}_1 = 22.0 V, \mathcal{E}_2 = 13.0 V, and R = 18. 0~ \Omega

For the junction rule, I_3 - I_1 - I_2 = 0

For the first loop, \mathcal{E}_1 - I_1(28.0) - I_3(18.0)=0

Solving for I_1 gives me I_1 = \frac{\mathcal{E}_1 - I_3(18.0)}{28.0}

For the second loop, \mathcal{E}_2 - I_2(12.0) - I_3(18.0)

Solving for I_2 gives me I_2 = \frac{\mathcal{E}_2 - I_3(18.0)}{12.0}

Taking I_1 and I_2, and substituting them into the equation for the junction rule, I get thatI_3 = 0.872. The true answer is 0.595. I did the calculation several times, but futile were the attempts. Have I applied Kirchhoff's incorrectly?

 

[gneill]

I am actually working on precisely the same problem, with the exception that \mathcal{E}_1 = 22.0 V, \mathcal{E}_2 = 13.0 V, and R = 18. 0~ \Omega

For the junction rule, I_3 - I_1 - I_2 = 0

For the first loop, \mathcal{E}_1 - I_1(28.0) - I_3(18.0)=0

Solving for I_1 gives me I_1 = \frac{mathcal{E}_1 - I_3(18.0)}{28.0}

For the second loop, \mathcal{E}_2 - I_2(12.0) - I_3(18.0)

Solving for I_2 gives me I_2 = \frac{mathcal{E}_2 - I_3}{12.0}

In that last equation, what happened to the 18.0 that multiplied I3 in the previous line?

 

[Bashyboy]

Whoops, I neglected to type that in--I'll fix it.

 

[gneill]

Whoops, I neglected to type that in--I'll fix it.

Did you then re-solve the simultaneous equations for I3?

 

[Bashyboy]

Yes, I substituted in I_1 and I_2, moved the terms that didn't have I_3 in them, and factored out I_3.

 

[gneill]

Yes, I substituted in I_1 and I_2, moved the terms that didn't have I_3 in them, and factored out I_3.

When I do that using your equations, I get the 0.595A result...

 

[Bashyboy]

I am still getting the same answer.

Here is my work:

I_3 - (\frac{\mathcal{E}_1 - I_3(18.0)}{28.0}) - (\frac{\mathcal{E}_2 -I_3(18.0)}{12.0}

I_3(\frac{18.0}{28.0} + \frac{18.0}{12.0}) = \frac{\mathcal{E}_1}{28.0} + \frac{\mathcal{E}_2}{12.0}

Finally,

I_3 = 0.872~A

 

[gneill]

I am still getting the same answer.

Here is my work:

I_3 - (\frac{\mathcal{E}_1 - I_3(18.0)}{28.0}) - (\frac{\mathcal{E}_2 -I_3(18.0)}{12.0}

I_3(\frac{18.0}{28.0} + \frac{18.0}{12.0}) = \frac{\mathcal{E}_1}{28.0} + \frac{\mathcal{E}_2}{12.0}

What about the "lone" I3 term on the left? Why did it disappear?

 

[Bashyboy]

What lone I3 term? I didn't intend for any to disappear.

I am still getting the same answer.

Here is my work:

I_3 - (\frac{\mathcal{E}_1 - I_3(18.0)}{28.0}) - (\frac{\mathcal{E}_2 -I_3(18.0)}{12.0}

I_3(\frac{18.0}{28.0} + \frac{18.0}{12.0}) = \frac{\mathcal{E}_1}{28.0} + \frac{\mathcal{E}_2}{12.0}

Once I got to this step, I divided both sides by \frac{18.0}{28.0} + \frac{18.0}{12.0}

Which gave me

Finally,

I_3 = 0.872~A

 

[gneill]

What happened to the first I3 term?

 

[Bashyboy]

Oh, I see...It should be (1 + 18.0/28.0 + 18.0/12.0). I kept neglecting the 1.

 

[gneill]

Oh, I see...It should be (1 + 18.0/28.0 + 18.0/12.0). I kept neglecting the 1.

Exactly