Finding determinant through Gaussian elimination

[purplecows]

If I switch 2 rows, do I have to multiple by -1 each time?

For example, I have

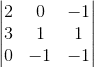
If I switch row 2 and 3, will it become this:

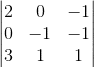
Or this?

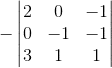
Each time I make a switch, do I have to also put a negative sign?

Edit: Not really related to Gaussian elimination, but this is from a Gaussian elimination problem; I just wanted to know whether I have to put a negative each time I make the switch.

 

[SteamKing]

It's not clear what switching rows does for you in terms of finding the determinant of this matrix.

Using the original matrix, you would want to eliminate element a21 = 3 first. After that, you can work on eliminating a32, leaving you with an upper triangular matrix. The determinant of an upper triangular matrix is easy to calculate.

FYI, the elementary row operations affect the determinant as discussed in the following article:

http://en.wikipedia.org/wiki/Gaussian_elimination

See the section 'Computing determinants' under Applications.

 

[HallsofIvy]

Actually, it is "clear what switching rows does for you in terms of finding the determinant of this matrix."

Anytime you swap two rows in a determinant, you multiply the determinant by -1.

In this case, the original determinant is $$\left|\begin{array}{ccc}2 & 0 & -1 \\ 3 & 1 & 1 \\ 0 & -1 & -1 \end{array}\right|$$. If you "expand by minors" on the first row, you get $$2\left|\begin{array}{cc}1 & 1 \\ -1 & -1\end{array}\right|- 1\left|\begin{array}{cc} 3 & 1 \\ 0 & -1\end{array}\right|= 2(-1+ 1)- (-3)= 3$$

Switching the first two rows you get $$\left|\begin{array}{ccc}3 & 1 & 1 \\ 2 & 0 & -1 \\ 0 & -1 & -1 \end{array}\right|$$. If you "expand by minors" on the second row, you get exactly the same thing except that, because your leading coefficients are from the second row, their sign is changed: $$-2\left|\begin{array}{cc}1 & 1 \\ -1 & -1\end{array}\right|+ 1\left|\begin{array}{cc} 3 & 1 \\ 0 & -1\end{array}\right|= -2(-1+ 1)+ (-3)= -3$$.

Switching the first and third rows and expanding on the third row will give you almost exactly the same thing. This time the leading coefficients will be the same as the first time but the two rows in the sub-determinants are reversed, reversing the sign there:
$$\left|\begin{array}{ccc}0 & -1 & -1\\ 3 & 1 & 1 \\ 2 & 0 & -1 \end{array}\right|$$. If you "expand by minors" on the third row, you get $$2\left|\begin{array}{cc}-1 & -1 \\ 1 & 1\end{array}\right|- 1\left|\begin{array}{cc} 0 & -1 \\ 3 & 1\end{array}\right|= 2(-1+ 1)- (3)= -3$$

 

[SteamKing]

Actually, it is "clear what switching rows does for you in terms of finding the determinant of this matrix."

That's fine, but the OP wanted to find the determinant of the matrix by using elimination, not by expanding minors. Switching rows as he did originally did not make his transformed matrix closer to upper triangular form; it complicated the elimination by adding extra steps.

To find the determinant of a 3x3 matrix is a trivial exercise anyway; one can always calculate the determinant using the formula of Sarrus.

 

[blue_raver22]

I can provide a response to this question from a mathematical perspective. When performing Gaussian elimination, switching two rows will not change the determinant of a matrix. This is because switching two rows is equivalent to multiplying the matrix by a permutation matrix, which has a determinant of either 1 or -1. So, if you switch two rows, you do not need to multiply by -1 each time.

In terms of the specific example given, switching row 2 and row 3 will result in the same determinant regardless of whether you switch the signs of the entries in the rows or not. This is because the determinant of a matrix is only affected by the order of the rows and not the actual values in the rows.

In summary, switching two rows in Gaussian elimination will not change the determinant, and therefore there is no need to include a negative sign each time you make a switch.