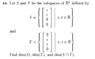Dimensions of Intersection of Matrices S and T

[pyroknife]

I've attached the problem.

For S:
I form the matrix:
1 0
0 1
0 0
0 0

Thus the dimension is 2.

For T:
I form the matrix
0 0
1 0
0 1
0 0
Thus the dimension is also 2.

Is that the correct idea?



Also what does S ∩ T mean? I couldn't find the symbol in my textbook.

 

[leej72]

Yes, the dimension for those matrices are 2, when talking about dimension we either talk about row or column dimension.
the S ∩ T means all the elements that are common in S and T.

 

[pyroknife]

What does common mean? A column that is included in both matrices?

 

[leej72]

Well in this case it would be the rows that both S and T have common elements in.
Hint: look past the parameters s,t

 

[pyroknife]

Hmmm I don't understand why in this case it would be rows?

The only row in common is the last row (0 0).

 

[leej72]

Hmmm I don't understand why in this case it would be rows?

The only row in common is the last row (0 0).

Sorry I misread your problem, since there are no common elements in each vector, there is no dimension for the intersection of S and T because they have no common elements

 

[HallsofIvy]

First "$\cap$" is the standard symbol for the "intersection" of two sets- it is the set contain all things that are in both sets. I am surprised that you are working with vector spaces but have not yet learned basic set terminology.

Second, this problem does NOT ask you to find the "intersection" of two vectors- vectors are not sets. It asks you to find the subspaces spanned by the two vectors. Any vector in S is of the form <a, 0, 0, 0> so this is a one dimensional space. In particular, it has second, third and fourth components 0. Any vector in T is of the form <0, b, 0, 0>. In particular, it has first, third and fourth components 0. Any vector in their intersection must be in both and so must sastisfy both conditions. The only vector that does that is <0, 0, 0, 0>, the zero vector. That is a subspace of dimension 0.

 

[pyroknife]

Aren't vectors in S of the form <s 0 0 0>and <0 t 0 0>
and vectors in T of the form <0 s 0 0> and <0 0 t 0>?

 

[HallsofIvy]

Yes, S is spanned by <1, 0, 0, 0> and <0, 1, 0, 0> and T is spanned by <0, 1, 0, 0> and <0, 0, 1, 0>. And since those are independent, they are bases for the subspaces so each has dimension 2.

The fact that <0, 1, 0, 0> is in both of those should make this problem of the intersection easy!

 

[pyroknife]

Oh so the dimension of S∩T is just 1.

 

[pyroknife]

For this case, when you say that the dimension of S∩T is one, would it be necessary to list the vector 0 1 0 0 as the one that exists in both? I guess I'm not sure how to to state it. I can obviously just say dim(S∩T)=1, but do I need to explain it in words or justify it?

 

[HallsofIvy]

Typically, with a problem of this kind you should justify your answer. Any vector in S is of the form a(1, 0, 0, 0)+ b(0, 1, 0, 0) and any vector in T is of the form c(0, 1, 0, 0)+ d(0, 0, 1, 0). Any vector that is in their intersection can be written both ways so we must have a(1, 0, 0, 0)+ b(0, 1, 0, 0)= c(0, 1, 0, 0)+ d(0, 0, 1, 0) for some numbers a, b, c, and d. That is the same as (a, b, 0, 0)= (0, c, d, 0) so we must have a= 0, b= c, d= 0.

(Be very careful with your wording. You cannot talk about "the vector that exists in both" because the intersection, being a subspace, contains an infinite number of vectors.)

 

[pyroknife]

Yeah, I just talked to my professor about it and he said the dimension is the size of a basis. By "size of a basis," does that just mean how many vectors span S∩T, which is likewise the dimension of S∩T. If so the basis of S∩T is spanned by the vector [ 0 1 0 0]^t. Thus the size of the basis is 1 and the dimension is 1.

Is that the right idea?

 

[pyroknife]

oops

 

[charlies1902]

I think you got it. [0 1 0 0]^t span both S and T, thus dim(SnT)=1.

I could be wrong though. Anyone else verify?

 

[charlies1902]

Hmmm. There's a relationship dim(U+V)=dim(U)+dim(V)-dim(U ∩ T)
Where U is your S and V is your T.
Dim(U+V)=2=2+2-dim(U ∩ T)
Which makes dim(U ∩ T)=2

 

[pyroknife]

hmmm That equation is saying there's 2, but i think hallsofivy says there's 1. I'm really confused. That equation does make sense tho, U+V is spanned by 2 linearly independent vectors.

 

[HallsofIvy]

Hmmm. There's a relationship dim(U+V)=dim(U)+dim(V)-dim(U ∩ T)
Where U is your S and V is your T.
Dim(U+V)=2=2+2-dim(U ∩ T)
Which makes dim(U ∩ T)=2

hmmm That equation is saying there's 2, but i think hallsofivy says there's 1. I'm really confused. That equation does make sense tho, U+V is spanned by 2 linearly independent vectors.

No, U+ V (Your S+ T) is spanned by three linearly independent vectors {< 1, 0, 0, 0>, <0, 1, 0, 0>, and <0, 0, 1, 0>, the three vectors you gave initially. So dim(U+ V)= 3, not two.
so dim(U+ V)= 3= 2+ 2- dim(U∩V)= 2+ 2- 1.

 

[pyroknife]

Oh I think I misunderstood the meaning of dim(U+V). I thought you add U+V then find the dimension.