Finding flux through a part of infinite disc

[Saitama]

Homework Statement

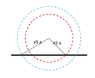
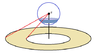
A charge $(5\sqrt{2}+2\sqrt{5})$ coulomb is placed on the axis of an infinite disc at distance $a$ from the centre of disc. The flux of this charge on the part of the disc having inner and outer radius of $a$ and $2a$ will be

A)$\dfrac{3}{2\epsilon_0}$

B)$\dfrac{1}{2\epsilon_0}$

C)$\dfrac{2(\sqrt{5}+\sqrt{2})}{\epsilon_0}$

D)$\dfrac{2\sqrt{5}+5\sqrt{2}}{2\epsilon_0}$

Answer: A

Homework Equations

The Attempt at a Solution

I have solved the given problem through integration but since this is an exam problem, I am wondering if there is a smarter way to solve this problem. Since the disc is infinite, I think we can use this fact to find a shorter method. Or is integration the only way to solve the problem?

Any help is appreciated. Thanks!

 

[TSny]

Did you integrate by breaking the annular region of the disk into nested rings and integrating the normal component of E over the rings?

If so, there is a trick you can do to set up a much simpler integral that will yield the result. (You can avoid actually doing this integration if you happen to know the formula for the surface area of a spherical cap (hint). But that's something I would have to look up )

 

[Saitama]

Did you integrate by breaking the annular region of the disk into nested rings and integrating the normal component of E over the rings?

Yes, that's exactly how I did it. :)

(You can avoid actually doing this integration if you happen to know the formula for the surface area of a spherical cap (hint). But that's something I would have to look up )

I think I understand your trick but I don't seem to able to apply it. Don't we have two spherical caps here? One of radius $\sqrt{2a^2}$ and the other of $\sqrt{5a^2}$.

 

[TSny]

I was thinking of working with a single sphere which you could take to be a sphere of unit radius. But, yes, there will be two spherical caps on this sphere to consider, if you want to avoid integration. Or, you can set up a simple integral on this sphere and not worry about looking up a formula for the area of a spherical cap.

 

[Saitama]

I was thinking of working with a single sphere which you could take to be a sphere of unit radius. But, yes, there will be two spherical caps on this sphere to consider, if you want to avoid integration. Or, you can set up a simple integral on this sphere and not worry about looking up a formula for the area of a spherical cap.

Umm...I don't get it, I have attached a figure, do I have to find the flux through the red spherical cap? I am thinking that I will have to deal with solid angle.

 

[TSny]

Draw a small sphere around the charge with a radius considerably smaller than $a$. You can think of it as having unit radius.

EDIT: Here's a pic

 

[Saitama]

Draw a small sphere around the charge with a radius considerably smaller than $a$. You can think of it as having unit radius.

EDIT: Here's a pic

Brilliant! That is such a nice method, thank you very much TSny! :)

How did you think of the sphere? And what's wrong with my spherical caps?

 

[TSny]

How did you think of the sphere? And what's wrong with my spherical caps?

I'm not sure how the thought came to me. Probably I've seen similar examples before. (I'm old)

Your spherical caps are just fine! It's a nice way and it will require about the same work as using a single sphere.

 

[Saitama]

Very sorry for the delay in reply, I did not have access to internet.

I'm not sure how the thought came to me. Probably I've seen similar examples before. (I'm old)

Can you please tell me where you saw these kind of examples? :)

Your spherical caps are just fine! It's a nice way and it will require about the same work as using a single sphere.

Yes, I reached the answer from my spherical caps too, thank you for the awesome solution TSny!

 

[sankalpmittal]

Very sorry for the delay in reply, I did not have access to internet.
Can you please tell me where you saw these kind of examples? :)Yes, I reached the answer from my spherical caps too, thank you for the awesome solution TSny!

This question was from FIITJEE AITS part test II. Are you giving this exam ? Same here. I was not able to solve this problem during exam. It was only at home that I solved it by manual integration.

But your method is awesome shortcut TSny ! Thanks ! :)

 

[TSny]

Can you please tell me where you saw these kind of examples? :)

I really can't say. You'll just pick up this sort of thing with practice.

Yes, I reached the answer from my spherical caps too

Good work!