Flux with an infinitely long surface cutting through a sphere

[mk9898]

Homework Statement

Bildschirmfoto 2018-06-19 um 18.50.50.png
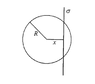
In the y-z plane there is an infinite long surface with charge density $\sigma$ that slices through a sphere with radius R. Determine the Flux.

The Attempt at a Solution

I have solved the problem but am stuck at the last part. I used Gauss and found that the flux is equal to $\frac{Q_{in}}{\epsilon_0}$ (per the theorem of course). But at the end I have to formulate it with sigma and the area. Something like:

$\frac{Q_{in}}{\epsilon_0} =\frac{\sigma A_{in}}{\epsilon_0}=...$

But my question is, what exactly is $A_{in}$? It is the area within the sphere? That would just be $\frac{4}{3}\pi r^3$ but that doesn't make much sense.

 

[TSny]

But my question is, what exactly is $A_{in}$? It is the area within the sphere?

Since you want the charge inside the sphere, $A_{in}$ is the area of the region of the infinite plane that is inside the sphere. What is the geometrical shape of this region of the plane?

That would just be $\frac{4}{3}\pi r^3$ but that doesn't make much sense.

No. This formula would give you the volume of a sphere of radius $r$.

 

[mk9898]

Since you want the charge inside the sphere, $A_{in}$ is the area of the region of the infinite plane that is inside the sphere. What is the geometrical shape of this region of the plane?

The geometrical shape looks similar to a football, right? The thing that is throwing me off, is that the charge could encompass the entire sphere on the left, but then there would be no symmetry on the right. So I figured that A would just be a cross section of the entire sphere:$\pi R^2$

I'm leaning towards the fact it is a football shape and that would lead to $A_in = \pi(R^2-x^2)$. But my concern with that, is that x is fixed. So from my photo if we moved the A_in (in blue) upward...it wouldn't be a football anymore it would just be a cylinder.

 

[mk9898]

Ok so I have found the answer:

http://physics-problems-solutions.blogspot.com/2014/03/electromagnetism-gauss-law_19.html

But why is the gaussian surface a circle around the plane?

 

[TSny]

But why is the gaussian surface a circle around the plane?

I believe that you want to find the electric flux through the surface of the sphere that has radius R. This wasn't too clear in the statement of the problem in post #1. Therefore, the gaussian surface will be the surface of this sphere. The flux through this surface equals the charge inside this surface divided by $\epsilon_0$.

The figure on the left is the original viewpoint where the infinite plane is seen edge-on, slicing through the sphere. The figure on the right shows looking perpendicularly into the infinite plane. The middle picture is an intermediate viewpoint.

 

[mk9898]

Ahhhhh! Wow I cannot thank you enough! I had a totally false idea of what it looked like. Thank you thank you. Now all of my questions are answered.

 

[TSny]

OK, glad that I could help.