You also have an equation which does not have the amplitude in it.
It's one equation with one unknown - you can solve it.
On notation:
x(0.3) means the value that x takes at t=0.3.
When you have a relation f(x)=g(x) it is asking for the intersection of f(x) with g(x).
f and g are two curves - if the solution exists, then they will intersect at one or more points.
Lets recap:
At ##t=0##, ##x(0)=x_0##, ##v(0)=v_0## ... which you are not given, so this is just notation.
At some time later: ##t=a##, ##x(a)=x_a##, ##v(a)=V_a## ... which you
are given. a=0.3 etc right?
If the mass is displaced by a distance A and ten released, then: ##x_0=A## and ##v_0=0##
And you have equations of motion:
(1) ##x(t)=A\cos\omega t## and (2) ##v(t)=-\omega A\sin \omega t##
(2)/(1) gives you:
##v(t)=-\omega x(t)\tan\omega t##
plug in your known values and divide through by the frequency:
$$\frac{v_a}{\omega} = -x_a\tan\omega t$$ (BTW: did you misplace a minus sign?)
This should be where you are up to - I've rearranged things a bit. Let me know if I've lost you.
Note:
you cannot get rid of the tan function.
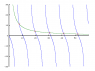
Anyway: this is an equation of the form ##f(\omega)=g(\omega)## ... i.e. the solutions are the values of ##\omega## where ##f(\omega)## intersects ##g(\omega)##.
Use your computer to draw you a graph of ##f## and ##g## vs ##\omega## and where those lines intersect are your solutions.
I'll start you off:
... above: the horizontal axis is frequency, the green line is f and the blue line is g
I've marked the solutions in with a red x.
Notice how the periodicity of the tangent function in g means there are an infinite number of solutions. Your prof seems to intend you to pick the first one ... you should be able to see the frequency is about 7rad/s ... you need more accuracy than that :)