Troi Jones
- 13
- 0
Homework Statement
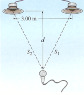
Two loudspeakers are placed 3.00 m apart horizontally.They emit 425 Hz sounds, in phase. A microphone is placed d= 3.20 mid distant from a point midway between the two speakers, where an intensity maximum is recorded.
(a) How far must the microphone be moved to the right to find the first intensity minimum?
(b) Suppose the speakers are reconnected so that the 455 Hz sounds they emit are exactly out of phase. At what positions (how far must the microphone be moved to the right) are the intensity maximum and minimum now?
Homework Equations
S1 - S2= wavelength/2
The Attempt at a Solution
I solved for lengths S_2 and S1 through the Pythagorean theorem which is sqrt(1.5^2 +3.2^2)= 3.534 m. But that's all I know so far. I do not have any other idea of where to go from here. Any type of guidance would be useful, understanding waves is my weak point.[/B]