Finding normal force from center of gravity

[thatgirlyouknow]

Homework Statement

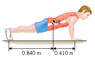
The figure shows a person whose weight is W = 725 N doing push-ups. Find the normal force exerted by the floor on (a)each hand and (b)each foot, assuming that the person holds this position.

Homework Equations

center of gravity = cg
Xcg = (W1x1 + w2x2 +...)/(w1 + w2...)
net torque = w1x1 + w2x2 +...

The Attempt at a Solution

Placing the axis of rotation at the far left gives:
W1(0) + W2(.84) + W3(1.25) / 725 = .84
Placing it at the far right gives:
W1(1.25) + W2(.41) + W3(0) / 725 = .41

Solving these yields W1 = [297.25 - W2(.41)]/1.25
or
W2 = 297.25 - W1(1.25)
and
W2(.84) + W3(1.25) = 609

However, there are still too many unknowns. Where do I take it from here?

 

[Doc Al]

Placing the axis of rotation at the far left gives:
W1(0) + W2(.84) + W3(1.25) / 725 = .84

Not quite sure what you're doing here. Looks like you're trying to calculate the center of gravity? But you are given the center of gravity.

Instead, set the net torque equal to zero for equilibrium.

Don't forget that the net force on the person must also be zero.

That will give you two equations and two unknowns.

 

[thatgirlyouknow]

So w1x1 + w2x2 + w3x3 = 0?

w1*.840 + w2*0 + w3*.41 = 0

w1+w2+w3 = 725

I get that the first equation has two unknowns, but what about the second?

 

[Doc Al]

So w1x1 + w2x2 + w3x3 = 0?

w1*.840 + w2*0 + w3*.41 = 0

Realize that the torques will have different signs.

w1+w2+w3 = 725

I get that the first equation has two unknowns, but what about the second?

Are all three Ws unknown?

 

[thatgirlyouknow]

They appear to be, unless I should assume that the middle one is 725 (the total weight.) Is this assumption correct?

 

[thatgirlyouknow]

Ok, I got it:
Set up as Fn1(0) + Fn2(.84) + Fn3(1.25) = 0
Fn2 = 725
so Fn3 = 487.2
Divided by 2 gives the hands, and the remainder is split between the feet.

 

[Doc Al]

Good.

Here's how I look at this problem. There are three forces acting on the person:
(1) The upward force at his feet: Ff
(2) The upward force at his hands: Fh
(3) The downward force of his weight: W (which is known)

So your torque equation becomes:
Ff(0) + W(.84) -Fh(1.25) = 0
Which you can solve for Fh:
Fh = W(.84)/(1.25)
(Note that clockwise and counterclockwise torques have different signs.)

And your net force equation is:
Ff -W + Fh = 0
Which you can solve for Ff in terms of W and Fh (which are known):
Ff = W - Fh